Проверка значимости линейного уравнения
Значимость уравнения определяется возможностью надежного прогноза результативного показателя по значениям факторных признаков. Значимость линейной регрессии проверяется по F–критерию Фишера, расчетное значение которого определяется согласно следующей формуле:
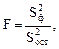 (1.8)
(1.8)
где 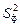 –факторная дисперсия результативного показателя (оценивает степень влияния изучаемого фактора на Y, т.е. объясняемую регрессию), которой соответствует число степеней свободы
–факторная дисперсия результативного показателя (оценивает степень влияния изучаемого фактора на Y, т.е. объясняемую регрессию), которой соответствует число степеней свободы 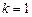 ,
,
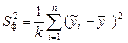 ; (1.9)
; (1.9)
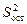 – остаточная дисперсия (характеризует воздействие неучтенных факторов, т.е. необъясняемую регрессию):
– остаточная дисперсия (характеризует воздействие неучтенных факторов, т.е. необъясняемую регрессию):
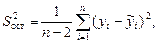 (1.10)
(1.10)
где 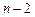 – число степеней свободы, соответствующее линейной регрессии.
– число степеней свободы, соответствующее линейной регрессии.
Если расчетное значение критерия больше табличного, выбираемого по теоретическим значениям F-распределения Фишера при заданном уровне значимости и двух степенях свободы 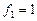 и
и 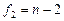 , то выдвинутая гипотеза о незначимости линейного уравнения регрессии не принимается.
, то выдвинутая гипотеза о незначимости линейного уравнения регрессии не принимается.
Для выбора лучшего уравнения регрессии (из множества значимых) могут быть использованы следующие критерии их качества:
· минимум остаточной дисперсии;
· минимум корреляционного отношения
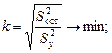 (1.11)
(1.11)
· минимум относительной ошибки аппроксимации
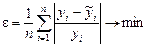 . (1.12)
. (1.12)
Уравнения регрессии затем ранжируются по данным критериям. Минимальная сумма баллов соответствует лучшему уравнению регрессии [2].
Оценивается значимость не только уравнения в целом, но и отдельных его параметров путем расчета их стандартных ошибок. Например, для линейной регрессии вида 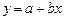 истинные значения параметров от рассчитанных по выборочным данным отличаются на следующие величины стандартных ошибок
истинные значения параметров от рассчитанных по выборочным данным отличаются на следующие величины стандартных ошибок
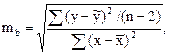

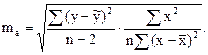
Доверительные границы Y при значении фактора 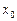 для линейной регрессии определяются по формуле
для линейной регрессии определяются по формуле
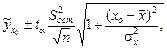 (1.13)
(1.13)
где 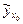 – значение Y, рассчитанное по уравнению регрессии при
– значение Y, рассчитанное по уравнению регрессии при 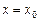 ;
;
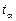 –табличное значение критерия Стьюдента при уровне значимости
–табличное значение критерия Стьюдента при уровне значимости 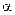 и числе степеней свободы
и числе степеней свободы 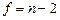 .
.
 2014-02-09
2014-02-09 441
441








