Степень нелинейной зависимости оценивается индексом корреляции R, величина которого может быть определена по следующей формуле
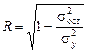 , (1.14)
, (1.14)
где 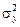 – общая дисперсия результативного показателя:
– общая дисперсия результативного показателя:
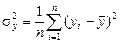 ;
;
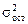 – остаточная дисперсия
– остаточная дисперсия
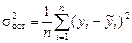 .
.
Оценка полученных значений основана на следующих свойствах данного коэффициента.
1. 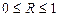 .
.
2. Если 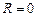 , то корреляционной зависимости между Y и фактором, положенным в основу группировки X, нет.
, то корреляционной зависимости между Y и фактором, положенным в основу группировки X, нет.
2. Если 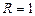 , то все точки корреляционного поля располагаются на кривой.
, то все точки корреляционного поля располагаются на кривой.
4. Чем ближе значение 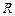 к 1, тем корреляционная зависимость сильнее.
к 1, тем корреляционная зависимость сильнее.
5.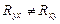 .
.
6.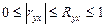 .
.
Если нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого совпадает с индексом корреляции, т.е.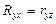 , где z – преобразованная (линеаризованная) величина. Если линеаризация связана с преобразованием не только фактора X, но и результата Y, то
, где z – преобразованная (линеаризованная) величина. Если линеаризация связана с преобразованием не только фактора X, но и результата Y, то 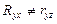 .
.
Значимость индекса корреляции проверяется также как и оценка надежности коэффициента корреляции (п.1.2). Для проверки значимости нелинейной регрессии используется индекс детерминации 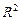 и критерий Фишера, расчетное значение которого может быть определено по следующей формуле:
и критерий Фишера, расчетное значение которого может быть определено по следующей формуле:
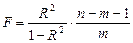 , (1.15)
, (1.15)
где 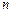 – объем выборки;
– объем выборки;
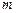 – число параметров при переменных
– число параметров при переменных 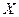 .
.
Расчетное значение критерия сравнивается с табличным, определяемым по таблицам соответствующего распределения в зависимости от уровня значимости и двух степеней свободы 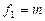 и
и 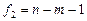 .
.
 2014-02-09
2014-02-09 732
732








