Оценка параметров уравнения множественной
Модель множественной регрессии может быть представлена в виде
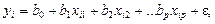 (2.5)
(2.5)
где 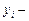 i -тое наблюдение результативного показателя;
i -тое наблюдение результативного показателя;
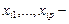
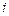 -ое наблюдение факторных признаков.
-ое наблюдение факторных признаков.
Включение в регрессионную модель новых объясняющих переменных усложняет полученные вычисления. Это приводит к целесообразности использования матричных обозначений:
а) Y – вектор-столбец зависимых переменных размерности n, т.е.
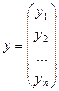 ;
;
б) Х – матрица значений объясняющих переменных размерности 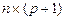 , значения элементов первого столбца которой объясняется тем, что
, значения элементов первого столбца которой объясняется тем, что 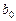 умножается на фиктивную переменную
умножается на фиктивную переменную 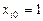 для всех i
для всех i
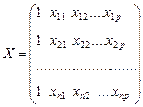 ;
;
в) B – матрица-столбец (вектор) параметров регрессии размерности p
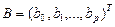 ;
;
г) 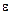 – вектор случайных ошибок размерности n
– вектор случайных ошибок размерности n
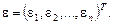
Тогда, в матричной форме модель (2.5) примет вид
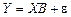 . (2.6)
. (2.6)
Для нахождения значений матрицы B (без учета вектора случайных ошибок) используют следующие преобразования выражения (2.6):
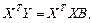
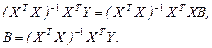
Для сравнительного анализа влияния факторов на изменение Y (в случае разных единиц измерения факторов) рассчитывают частные коэффициенты эластичности (формула (2.4)).
Расчет значений параметров уравнений регрессии может быть упрощен за счет использования выборочных частных коэффициентов корреляции и средних квадратичных отклонений. Так, для уравнения вида 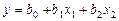 параметры
параметры 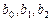 могут быть найдены по формулам
могут быть найдены по формулам
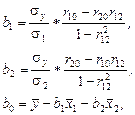
где 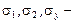 средние квадратичные отклонения признаков
средние квадратичные отклонения признаков 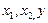 соответственно;
соответственно;
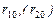 – частные коэффициенты корреляции между результативным признаком Y и первым (вторым) фактором соответственно;
– частные коэффициенты корреляции между результативным признаком Y и первым (вторым) фактором соответственно;
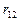 – частный коэффициент корреляции между признаками
– частный коэффициент корреляции между признаками 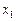 и
и 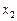 .
.
 2014-02-09
2014-02-09 448
448








