2014-02-09
1046
Для более точного и достоверного отражения действительности в модели необходимо подобрать такую форму кривой, которая бы адекватно отражала связи между факторами. Если форма кривой неизвестна, то можно аппроксимировать эту связь полиномом n -ой степени, считая его универсальной формой связи:
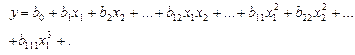(2.7)
На практике степень полинома и количество его параметров ограничивают, т.к. это не приводит к адекватному повышению точности расчетов. При увеличении количества параметров до числа, равного числу наблюдений, теоретическая линия регрессии будет проходить через все точки корреляционного поля, т.е. корреляционная зависимость станет функциональной, в которой будут учитываться не средние, а частные, случайные явления, при этом могут не учитываться принципиально важные характеристики самого объекта.
При аппроксимации нелинейной зависимости полиномом n -ой степени каждый его параметр заменяется условной переменной 1-ой степени и дальнейшие расчеты ведут по методике аппроксимации линейной зависимости:
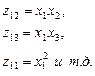
Тогда уравнение (2.7) сводится к виду
.
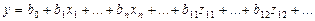Громоздкость полученной модели требует исключения из полинома отдельных его параметров без снижения точности аппроксимации. Решается эта задача путем многошагового регрессионного анализа в следующей последовательности.
1. Выбирается наиболее простая форма зависимости, например,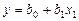 
.
2. Составляется система нормальных уравнений вида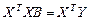 
и оцениваются параметры 
.
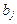3. Рассчитываются теоретические значения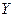 
по уравнению регрессии 
.
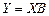4. Проверяется значимость уравнения регрессии по F-критерию Фишера. Если уравнение оказалось незначимым, то расширяется матрица X (соответственно, усложняется уравнение регрессии) и осуществляется переход к этапу 2. Если значимость доказана, то оценивают значимость отдельных коэффициентов регрессии, для чего определяют расчетные значения t - критерия Стьюдента по следующим формулам:
а) при одномерном регрессионном анализе:
;
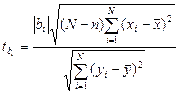б) при множественной корреляции:
,
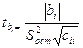где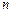 
– количество параметров уравнения регрессии;
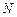– объем выборки;
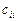– диагональный элемент матрицы 
,
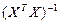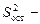остаточная дисперсия (формула (1.10)).
5. Расчетные значения критериев сравниваются с табличными при числе степеней свободы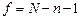 
. Коэффициенты считаются значимыми, если полученные значения не меньше табличных. Если это условие не выполняется, то в матрице X расширенного состава вычеркиваются соответствующая строка и столбец. Далее возвращаются ко второму этапу, и расчеты продолжают до тех пор, пока не будут исключены незначимые коэффициенты из уравнения регрессии.
