Под идентификацией понимается единственность соответствия между приведенной и структурной формами модели. Данная проблема возникает при переходе от приведенной формы к структурной по той причине, что структурная модель в полном виде, т.е. состоящая в каждом уравнении системы из 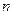 эндогенных переменных и
эндогенных переменных и 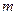 экзогенных переменных, содержит
экзогенных переменных, содержит 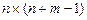 параметров, а приведенная форма –
параметров, а приведенная форма – 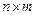 параметров. Таким образом, необходимо либо уменьшить количество параметров в структурной модели ввиду достаточно слабой зависимости некоторых X и Y, либо приравнять некоторые коэффициенты друг к другу или же ввести ограничения вида
параметров. Таким образом, необходимо либо уменьшить количество параметров в структурной модели ввиду достаточно слабой зависимости некоторых X и Y, либо приравнять некоторые коэффициенты друг к другу или же ввести ограничения вида 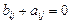 .
.
С точки зрения идентифицируемости различают следующие виды структурных моделей:
· идентифицируемые,когда все структурные коэффициенты определяются единственным образом по коэффициентам приведенной модели (число их параметров совпадает);
· неидентифицируемые,если число коэффициентов приведенной формы меньше числа структурных коэффициентов;
· сверхидентифицируемые,если число приведенных коэффициентов больше количества структурных элементов.
Система считается идентифицируемой, если каждое ее уравнение идентифицируемо, т.е., если хотя бы одно уравнение неидентифицируемо, то вся модель считается неидентифицируемой.
Если 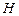 – число эндогенных переменных в j -том уравнении системы, а D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение, то условия можно представить следующим образом:
– число эндогенных переменных в j -том уравнении системы, а D – число экзогенных переменных, которые содержатся в системе, но не входят в данное уравнение, то условия можно представить следующим образом:
а) 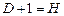 – уравнение идентифицируемо;
– уравнение идентифицируемо;
б) 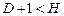 – уравнение неидентифицируемо;
– уравнение неидентифицируемо;
в) 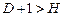 – уравнение сверхидентифицируемо.
– уравнение сверхидентифицируемо.
 2014-02-09
2014-02-09 455
455








