Оценка параметров структурной модели

Оценка параметров структурной модели осуществляется различными способами в зависимости от вида структурной модели.

1. Метод максимального правдоподобия с полной информацией – считается наиболее общим. Его результаты совпадают с обычным МНК, если X и Y подчиняются нормальному закону распределения. Недостаток: трудоемкость, громоздкость в случае больших систем.

2. Метод максимального правдоподобия (наименьшего дисперсионного отношения) при ограниченной информации. В отличие от предыдущего метода в нем снимаются ограничения, накладываемые на нормальность распределения. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой.

3. Косвенный МНК – применяется только в случае полной идентифицируемости модели. Процедура его применения может быть представлена следующим образом.

Первый этап: структурная модель преобразуется в приведенную форму.

Второй этап: для каждого уравнения приведенной формы коэффициенты 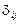оцениваются обычным МНК.

Третий этап: коэффициенты приведенной формы трансформируются в параметры структурной модели.

Рассмотрим структурную модель

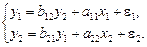(6.3)

Регион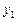
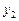
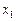
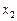
средние		6,2	2,4	3,4

Соответствующая приведенная форма модели имеет вид:

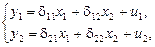(6.4)

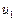где и 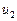– случайные ошибки приведенной формы модели.

Для каждого уравнения этой системы применяется традиционный МНК. Для упрощения расчетов работают с отклонениями от средних, т.е. 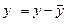и .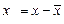

Например, для первого уравнения системы (6.4) критерий и соответствующие уравнения могут быть представлены следующим образом (без учета ошибок):

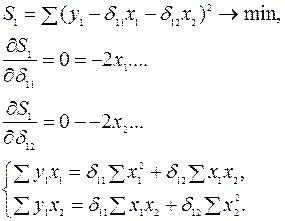
Решая данную систему по эмпирическим значениям 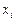и 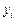(точнее, по отклонениям от их средних) можно оценить параметры приведенной формы 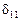и . Для второго уравнения системы (6.4) выполняются аналогичные преобразования, позволяющие в итоге оценить параметры 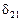и 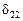. Таким образом, составляется система по приведенной форме (6.4). Далее, для перехода к структурной форме (к системе (6.3)) из первого уравнения полученной приведенной формы исключают 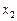, выразив его из второго уравнения приведенной формы и подставив его в первое. Эти преобразования позволят идентифицировать теоретическое значение 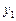. Для составления модели, позволяющей рассчитать 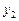(система (6.3)), из второго уравнения приведенной формы необходимо исключить 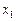, выразив его из первого уравнения и подставив во второе.

По примеру

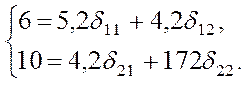
Решая данную систему, получим следующее первое уравнение приведенной формы модели:

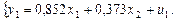
Аналогично применим МНК для второго уравнения приведенной формы модели, получим: