Данный метод применяется для сверхидентифицируемых систем, т.к. косвенный МНК в данном случае не позволяет получить однозначных оценок параметров. Основная задача двухшагового МНК (ДМНК) заключается в том, чтобы на основе приведенной формы модели рассчитать для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Решается данная задача в следующей последовательности.
1. Построение приведенной формы модели и нахождение на ее основе теоретических значений эндогенных переменных сверхидентифицируемого уравнения вида 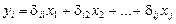 .
.
2. Определение структурных коэффициентов модели по расчетным (теоретическим) значениям эндогенных переменных.
Сверхидентифицируемая система может быть двух видов:
· все уравнения сверхидентифицируемы;
· хотя бы одно уравнение сверхидентифицируемо, а остальные – точно идентифицируемы.
ДМНК применяется к системам первого вида. Во втором случае структурные коэффициенты точно идентифицируемых уравнений определяются из системы приведенных уравнений.
Применим ДМНК к простейшей сверхидентифицируемой системе
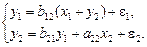
Данная модель может быть получена из модели (6.1), если наложить ограничения на ее параметры, а именно 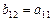 .
.
В результате, для первого уравнения 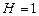 и
и 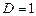 , т.е. оно стало сверхидентифицируемо; для второго уравнения
, т.е. оно стало сверхидентифицируемо; для второго уравнения 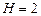 и
и 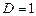 , следовательно, оно осталось точно идентифицируемым.
, следовательно, оно осталось точно идентифицируемым.
На первом шаге найдем приведенную форму модели, т.е.
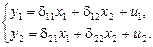
По эмпирическим данным (по аналогии с предыдущим разделом) оцениваются коэффициенты этой приведенной формы. На основе второго уравнения полученной приведенной модели необходимо найти теоретическое значение эндогенной переменной 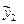 . С этой целью во второе уравнение приведенной формы подставляются значения
. С этой целью во второе уравнение приведенной формы подставляются значения 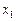 и
и 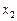 (или их отклонения от средних).
(или их отклонения от средних).
В сверхидентифицируемое уравнение подставляется новая переменная 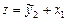 . Далее применим МНК к уравнению
. Далее применим МНК к уравнению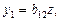 а именно
а именно
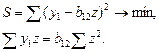
Откуда
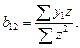
Для точно идентифицируемых уравнений результаты ДМНК совпадают с результатами косвенного МНК.
 2014-02-09
2014-02-09 588
588








