авторегрессионных моделей
Для прогнозирования рекомендуется использовать только значимые уравнения регрессии. Реализация данного метода сводится к определению прогнозного значения результативного показателя по прогнозируемым значениям факторов, которые, в свою очередь, могут определяться различными методами (на основе экстраполяции, экспоненциального сглаживания и т.д.).
Качество прогноза проверяется апостериорно и оценивается с помощью абсолютных и относительных ошибок (по аналогии с экстраполяцией).
Точечный прогноз может быть дополнен интервальной оценкой предсказанного значения результативного показателя в соответствии с формулой (1.13) для линейных трендов.
Прогнозирование по авторегрессионным моделям осуществляется поэтапно, т.е. со сдвигом на один уровень временного ряда вперед, и используется, главным образом, для предсказания случайной составляющей динамического ряда.
Пусть в анализируемом периоде n наблюдений. Тогда

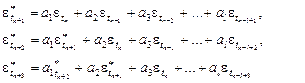
и т.д.,
где 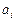 – коэффициенты авторегрессионной модели;
– коэффициенты авторегрессионной модели;
l – порядок авторегрессионной модели.
Границы доверительного интервала можно оценить следующим образом:
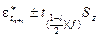 ,
,
где 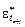 – результат точечного прогноза;
– результат точечного прогноза;
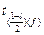 – квантили распределения Стьюдента при заданной доверительной вероятности p и числе степеней свободы
– квантили распределения Стьюдента при заданной доверительной вероятности p и числе степеней свободы 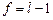 ;
;
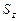 – среднеквадратическое отклонение, рассчитанное для случайных остатков авторегрессионной модели
– среднеквадратическое отклонение, рассчитанное для случайных остатков авторегрессионной модели
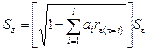 ,
,
где 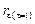 – значение автокорреляционной функции, вычисленное для
– значение автокорреляционной функции, вычисленное для 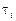 (значения лага),
(значения лага), 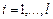 ;
;
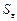 – среднеквадратическое отклонение для эмпирического динамического ряда
– среднеквадратическое отклонение для эмпирического динамического ряда 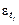 .
.
Абсолютная ошибка прогноза 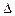 , таким образом, определяется как
, таким образом, определяется как
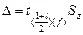 .
.
Относительную ошибку прогноза можно рассчитать по формуле
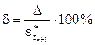 .
.
 2014-02-09
2014-02-09 525
525








