МАТЕМАТИЧЕСКОЕ ВЫРАЖЕНИЕ II ЗАКОНА
а.) Математическое выражение II закона термодинамики для обратимых процессов можно получить двумя способами:
1. 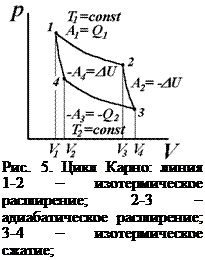 способ рассмотрения цикла Карно;
способ рассмотрения цикла Карно;
2. применение принципа Каратеодори (не рассматриваем).
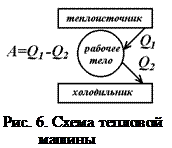
При рассмотрении цикла Карно (рис. 5), установлена теорема Карно–Клаузиуса: коэффициент полезного действия (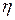 ) тепловой машины не зависит от природы рабочего тела (идеальный газ, пар, воздух и т.п.), а определяется только интервалом температур, в котором совершается работа. Это еще одна формулировка II закона термодинамики.
) тепловой машины не зависит от природы рабочего тела (идеальный газ, пар, воздух и т.п.), а определяется только интервалом температур, в котором совершается работа. Это еще одна формулировка II закона термодинамики.
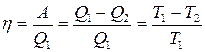 ;
;
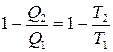 ;
;
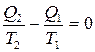 или
или 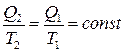 .
.
Из последнего уравнения следует, что отношение 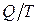 не зависит от пути протекания процесса, а определяется только начальным и конечным состоянием системы, т.е. является функцией состояния, обозначим
не зависит от пути протекания процесса, а определяется только начальным и конечным состоянием системы, т.е. является функцией состояния, обозначим 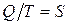 – энтропия. Термин энтропия ввел Клаузиус.
– энтропия. Термин энтропия ввел Клаузиус.
Энтропия – это отношение теплоты изотермического процесса к температуре процесса (приведенная теплота).
В обратимом процессе изменения энтропии не происходит.
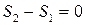 .
.
Для бесконечно малого цикла Карно запишем:
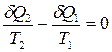 или
или 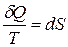 .
.
Таким образом, используя цикл Карно, получили математическое выражение II закона термодинамики для обратимых равновесных процессов в идеальном газе.
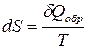 или
или 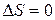 . (44)
. (44)
Важнейшим следствием из II закона термодинамики является вывод о существовании энтропии как термодинамической функции состояния.
Можно доказать, что уравнение II закона термодинамики (44) применимо к любым обратимым процессам в любых термодинамических системах.
б.) Получим математическое выражение II закона термодинамики для необратимого процесса.
Для этого запишем уравнение I закона термодинамики для произвольного термодинамического процесса, протекающего между одними и теми же исходным и конечным состояниями системы, необратимо и обратимо (или наоборот).
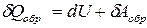 . (45)
. (45)
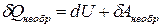 . (46)
. (46)
Вычтем почленно из уравнения (45) уравнение (46), получим:
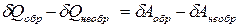 . (47)
. (47)
Согласно уравнению (43)
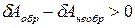 .
.
Следовательно, из (47) получаем:
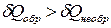 .
.
Подставим значение 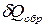 из (44), получим
из (44), получим
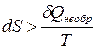 или
или 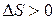 . (48)
. (48)
(48) – уравнение II закона термодинамики для необратимых процессов.
Часто уравнения (44) и (48) объединяют в одно уравнение и записывают:
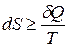 или
или 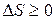 (49)
(49)
Из анализа уравнения (43) вытекает также, что работа обратимого процесса является максимальной работой процесса:
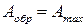 .
.
где 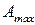 – работа данного процесса, протекающего обратимо.
– работа данного процесса, протекающего обратимо.
 2014-02-12
2014-02-12 692
692








