2014-02-12
5291
Частным случаем формул Стокса для двухмерных полей является формула Грина.
Теорема. Если векторная функция a = ax (x,y) i + ay (x,y) j непрерывна вместе со своими производными 
и 
в замкнутой области 
, то:
(7.11)
Замечание 5. Формула Грина имеет огромное самостоятельное значение в математике и довольно широко применяется в различных приложениях векторного анализа. Отметим, что впервые формула (7.11) появилась еще у Л. Эйлера в 1771 г., однако полный вывод этой формулы (вместе с другими формулами) и ее значение было дано английским физиком и математиком Дж. Грином в 1828 г.
Пример 7.7. С помощью формулы Грина вычислить криволинейный интеграл
,
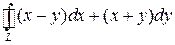где L – окружность x 2+ y 2= R 2.
Решение. Функции ax=x – y, ay=x + y,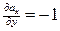 
, 
непрерывны в замкнутом круге: x 2+ y 2£ R 2. Следовательно, можно применить формулу Грина:
.
Заметим, что данный интеграл легко вычисляется непосредственно. Без использования формулы Грина.
Пример 7.8. Вычислить работу векторного поля
a =(x + y)2 i –(x–y)2 j
при перемещении материальной точки вдоль оси Ox и вдоль синусоиды y =sin x (0£ x£ p) против часовой стрелки (см. рис.7.4).
Решение. Поскольку функции ax= (x + y)2, ay=– (x – y)2, 
, 
непрерывны в рассматриваемой области, то по формуле Грина получаем
.
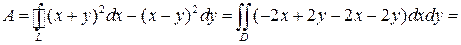
Из формулы Грина вытекают некоторые полезные формулы для вычисления площади области. Пусть D – некоторая область с границей L и S – площадь этой области. Известно, что двойной интеграл 
при f(x,y)º1 выражает площадь области D. Поэтому, если в формуле Грина подобрать функции ax (x,y) и ay (x,y) таким образом, чтобы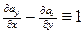 
, то площадь S области D, будет определяться формулой
.
Положим ay (x,y)=– x и ax (x,y)=0, тогда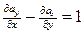 
и 
. Полагая ax (x,y)=– y и ay (x,y)=0, аналогично находим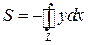 
, а при ax (x,y)=– y /2 и ay (x,y)= x /2 получим
. (7.12)
Пример 7.9. Используя формулу Грина, найти площадь фигуры, ограниченной эллипсом.
Решение. Используя параметрические уравнения эллипса: x=a cos t, y=b sin t (0£ t £2p), получим dx =– a sin tdt, dy = b cos tdt и далее, по формуле (7.12):
.
