Доказательство.Пусть существует. (Она одинакова по всем направлениям) Вычислим эту производную как предел в точке по направлению, параллельному оси

.

Далее аналогично и/или используя формулу Коши-Римана.

Замечание. Проще вычислять производные не по формуле, а по свойствам аналитических ФКП, которые будут перечислены ниже.

Определение. Функция называется аналитической в точке 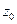, если она дифференцируема в некоторой окрестности этой точки.

Функция аналитическая в области 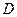, если она аналитична в каждой точке этой области и обозначается 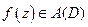, где 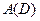- пространство аналитических функций в области .

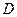Чтобы найти область аналитичности, надо узнать, в какой области 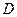она дифференцируема. (Но это трудоёмко.)