Дифференцируемость и аналитичность ФКП

Определение. Пусть задана ФКП 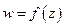. Производной 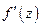этой функции в точке 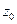называется предел

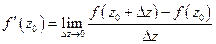, если этот предел существует и конечен. В этом случае функция называется моногенной или дифференцируемой (в комплексном смысле) в точке .

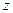Определение. Вещественно-значная Функция двух переменных 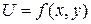называется дифференцируемой в точке 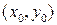, если в некоторой окрестности этой точки она может быть представлена в виде

,

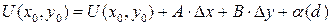где 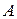и - ,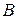

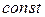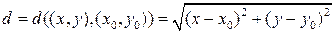
и 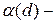б.м. более высокого порядка малости, чем 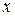, при .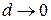

ТЕОРЕМА (Коши-Римана). Пусть функция 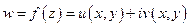определена в некоторой окрестности точки 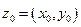. Для моногенной функции 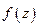в точке 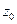необходимо и достаточно одновременного выполнения двух условий:

1) Функци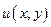и и 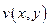дифференцируемы в точке 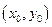(Как действительно-значные)

2) В точке 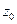выполняется условие Коши-Римана (Даламбера-Эйлера):

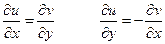
(без доказательства).

Утверждение 1. Формулы для производной