.
Глава 2. ИНТЕГРАЛ ОТ ФКП. РЯДЫ ТЕЙЛОРА И ЛОРАНА.
§1. Интеграл Коши (от ФКП)
Определение. Кривая 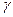 на комплексной плоскости
на комплексной плоскости 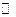 - отображение
- отображение 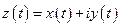 , где
, где 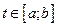 .
.
Если 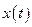 и
и  - непрерывные кусочно-гладкие функции, то
- непрерывные кусочно-гладкие функции, то 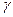 - непрерывная кусочно-гладкая кривая.
- непрерывная кусочно-гладкая кривая.
Определение. Пусть дано разбиение кривой 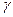 точками
точками 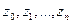 .
. 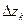 - длина дуги
- длина дуги 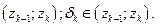
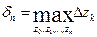 - максимальная длина участка разбиения дуги.
- максимальная длина участка разбиения дуги.
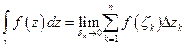 (1)
(1)
- интеграл от ФКП 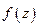 , если этот предел существует и конечен.
, если этот предел существует и конечен.
Выразим интеграл Коши (1) через криволинейные интегралы от функций действительных переменных.
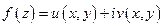 .
.
 .
.
 (2)
(2)
В правой части формулы – криволинейные интегралы 2 рода.
Из формулы (2) из соответствующих свойств криволинейных интегралов вытекают основные свойства интеграла от ФКП:
1) Линейность. (Не нуждается в пояснениях)
2) Аддитивность по путям интегрирования.
3) 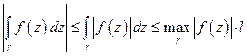 , где
, где 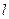 - длина кривой
- длина кривой 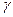 .
.
4) Равномерный предел 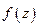 последовательности непрерывных функций
последовательности непрерывных функций 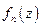 интегрируем и
интегрируем и 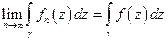 .
.
5) Замена переменной происходит аналогично действительным криволинейным интегралам.
§2. Теорема Коши (Интегральная)
ТЕОРЕМА 1. (Коши) Пусть дана функция 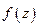 , аналитичная в области
, аналитичная в области 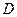 .
. 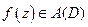 .
.
Тогда интеграл от 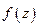 по любому замкнутому несамопересекающемуся кусочно-гладкому контуру
по любому замкнутому несамопересекающемуся кусочно-гладкому контуру 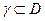 равен 0:
равен 0:
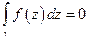 .
.
Замечание. Такой контур (несамопересекающийся, кусочно-гладкий) будем называть кривой Жордано. (Без доказательства)
ТЕОРЕМА 2. (Обобщённая теорема Коши) Пусть 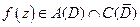 (т. е. аналитичная в
(т. е. аналитичная в 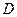 и непрерывная в
и непрерывная в 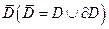 .
. 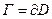 - Жорданова кривая. Тогда
- Жорданова кривая. Тогда
(Без доказательства)
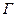
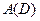

ТЕОРЕМА 3. (Интегральная формула Коши) Пусть 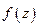 аналитична в
аналитична в 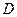 , где
, где 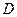 - односвязная область, её граница
- односвязная область, её граница 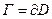 - кусочно-гладкая Жорданова кривая,
- кусочно-гладкая Жорданова кривая, 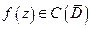 . Тогда
. Тогда
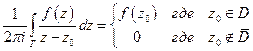
(Верхний случай – точка внутри области. Нижний – точка вне области. Доказательство нулевого результата вытекает из теоремы 2. В случае принадлежности точки к границе области (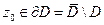 ) на пути интегрирования попадается сильная неинтегрируемая особенность (В одной из точек придётся делить на 0, невозможно взять интеграл Коши). Этот случай в данном курсе не рассматривается.)
) на пути интегрирования попадается сильная неинтегрируемая особенность (В одной из точек придётся делить на 0, невозможно взять интеграл Коши). Этот случай в данном курсе не рассматривается.)
Пример. Вычислить 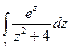 в случаях а)
в случаях а)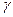 охватывает
охватывает 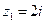 , но не включает
, но не включает 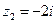 . б) Наоборот в)Охватывает обе точки
. б) Наоборот в)Охватывает обе точки
Решение. а)По интегральной формуле Коши 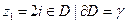 .
.
Получим 
б)Аналогично
 в)Разделим особенности
в)Разделим особенности
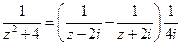

Можно разбить контур на два более простых (с общей границей) и проинтегрировать по каждому.
Некоторые следствия
ТЕОРЕМА 4. (Ллувилля) Если функция 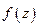 аналитична и ограничена на по модулю на всей комплексной плоскости, то она постоянна.
аналитична и ограничена на по модулю на всей комплексной плоскости, то она постоянна.
( )
)
Доказательство: 1)Сначала оценим интеграл, используя интегральную формулу Коши.
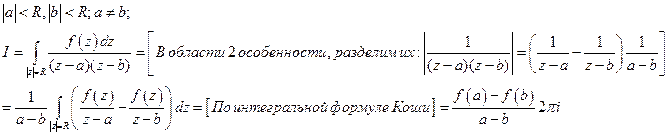 С другой стороны из свойств интеграла получим:
С другой стороны из свойств интеграла получим:
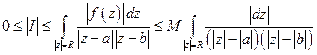
Т. к.  , а
, а 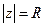 (это длина окружности), по теореме об интегральном среднем выносим максимум.
(это длина окружности), по теореме об интегральном среднем выносим максимум.
2)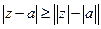 по свойствам модуля.
по свойствам модуля.
 , т. е.
, т. е.  для произвольных
для произвольных  .
.
Степенные ряды, в том числе ряды Тейлора, на действительной оси и на комплексной плоскости имеют много общего и верны основные результаты:
Для разложения ФКП в ряд Тейлора лучше пользоваться стандартными разложениями.
Наиболее близок к степенному ряду ряд вида
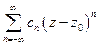 (1)
(1)
- ряд Лорана (по степеням 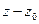 или относительно точки
или относительно точки 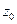 ).
).
ТЕОРЕМА 1. (Лорана) Пусть функция 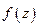 аналитична в кольце
аналитична в кольце  . Тогда внутри
. Тогда внутри 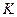 (т. е. для любой точки
(т. е. для любой точки 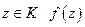 разлагается в ряд Лорана
разлагается в ряд Лорана

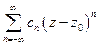 , где
, где
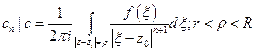
Замечания: 1) В окрестности бесконечно удалённой точки 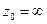 функция разлагается в ряд Лорана по степеням
функция разлагается в ряд Лорана по степеням 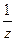 , т. е. функция
, т. е. функция 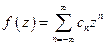 .
.
2) В окрестности конечной точки 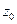 можно выделить
можно выделить  .
.
Здесь первая сумма – главная (иррегулярная) часть ряда Лорана, вторая сумма – правильная (регулярная) часть ряда Лорана. Поведение иррегулярной части тяжело описать аналитически.
По ряду Лорана будем судить об аналитичности функции в точке.
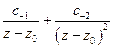 - имеем ошибку деления на 0 в
- имеем ошибку деления на 0 в 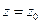 .
.
3)Относительно точки 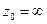 имеем
имеем
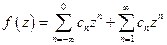 ,
,
Где первая сумма – правильная часть ряда, 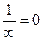 ; вторая сумма – главная часть ряда Лорана, даст особенности на бесконечно удалённой точке.
; вторая сумма – главная часть ряда Лорана, даст особенности на бесконечно удалённой точке.
Упражнение (Пример 2). Разложить функцию 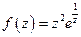 в ряд Лорана в окрестности точки а)
в ряд Лорана в окрестности точки а) б)
б)  , в обоих случаях выделить главную и правильную части.
, в обоих случаях выделить главную и правильную части.
Решение. 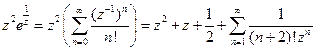
а)  .
. 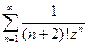 - главная часть, на нуле обращается в
- главная часть, на нуле обращается в 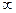 .
.
б)  . В
. В 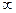 обращаются
обращаются  .
.
 2014-02-12
2014-02-12 1857
1857







