Достаточный признак аналитичности функции в области

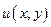Пусть и 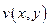непрерывны вместе со своими ЧП 1 порядка в области 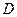, а так же удовлетворяют условиям Коши-Римана для всех 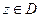. Тогда 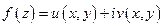аналитична в .

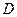Пример 1. .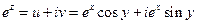

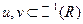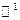. ( - область, где соблюдается непрерывность ЧП 1 порядка)

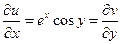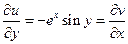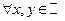, - оба условия выполнены, следовательно 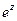аналитична на всей комплексной плоскости, .

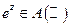ТЕОРЕМА 2. Сумма, разность, произведение и частное (Если знаменатель не обращается в 0) аналитических в точке (области) ФКП также является аналитической ФКП.

ТЕОРЕМА 3. Пусть функция 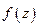аналитическая в точке 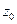, а функция 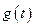аналитическая в точке 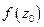. Тогда функция 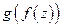аналитическая в точке .

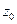Замечание. Действительная и мнимая части аналитической функции являются сопряжёнными гармоническими функциями.

Аналитическая функция с точностью до произвольной постоянной однозначно восстанавливается по своей действительной (мнимой) части при помощи условий Коши-Римана.