2014-02-12
1100
Рассмотрим бесконечную последовательность комплексных чисел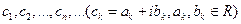 
Утверждение. Последовательность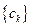 
сходится тогда и только тогда, когда одновременно сходятся 
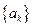и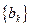 
.
Определение. Число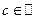 
называется пределом последовательности 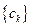и обозначается 
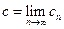, если 
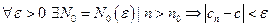. (То есть расстояние от элемента последовательности до предела меньше 
)
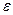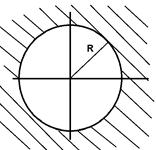
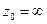называется пределом последовательности 
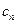, если 
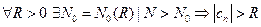. (Окрестность бесконечности, 
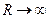- заштрихованная область)
Видим, что сходимость последовательности комплексных чисел сводится к сходимости двух последовательностей действительных чисел.
Утверждение.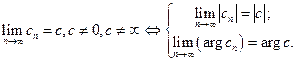 
(Чтобы последовательность КЧ сходилось к конечному числу, должны сходиться модуль и аргумент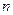 
-го элемента)
Пример 1. Возьмём последовательность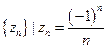 
. Какой бы радиус 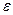мы не взяли, с некоторого номера в область 
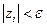станут попадать элементы последовательности. (
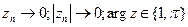- видим, что каждый следующий элемент всегда меняет значение аргумента, последовательность не стремится к какому-либо конкретному числу.
Упражнение 2. Доказать, используя определение предела: а)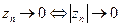 
. б) 
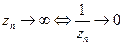. в)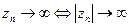 
.
|
|
|
Доказательство. а)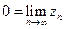 
,
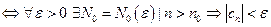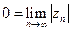
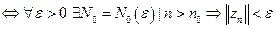- условия равносильны, выр-я эквивалентны.
б)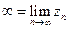 
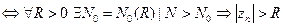
(Переобозначаем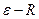 
) 
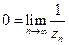
- снова эквивалентные условия.
в)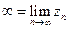
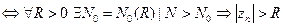
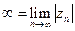
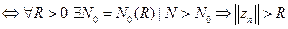-аналогично.
Аналогично вопросы сходимости рядов, составленных из комплексных чисел, сводятся к изучению сходимости рядов, составленных отдельно из действительных и мнимых частей.
