Замена переменного

Таблица неопределенных интегралов

Свойства неопределенного интеграла

1) 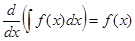, в частности,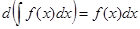

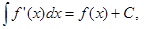
2) 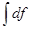=f+C

3) 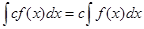, с точностью до аддитивной постоянной.

4) 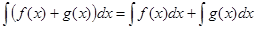, с точностью до аддитивной постоянной.

1) 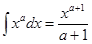+ С, a ¹ - 1.

2) 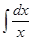= ln|x| + С, X={x>0} или X={ x<0 }, но не на X=(-¥,0)È(0,¥)

3) 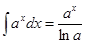+ C, a¹1, 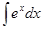=e^x+C

4) 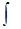sin x dx = - cos x + C, 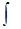cos x dx = sin x + C

5) ,

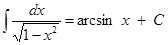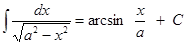
6) 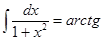x 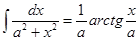+ C, + C

7) 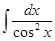=tg x + C, 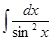=-ctg x + C

8) 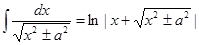+ C

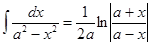9) + C

10) 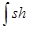x dx = ch x + C, 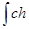x dx = sh x + C

11) 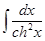= th x + C, 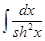= -cth x + C

§2. Два основных метода интегрирования

Если F(x) – первообразная для f(x) на X т.е. 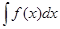= F(x)+C, если x=j(t) дифференцируема на T и определена суперпозиция 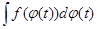= F(j(t))+C, тогда функция F(t)=f(j(t))j¢(t) имеет первообразную, равную F(j(t)). Таким образом,

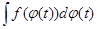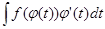= (формула замены переменного).

Для доказательства достаточно продифференцировать левую и правую части и убедиться, что получится одна и та же функция.

Примеры:

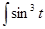cos t dt = 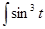d sin t = 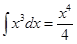+ C, x = sin t.

J = 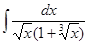, сделаем замену x = t⁶, тогда

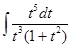J=6=6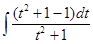=6t – 6 arctg t + C =6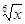-6 arctg 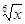+C