2014-02-12
1060
Общее решение задачи Джонсона методом ветвей и границ.
Пусть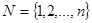 
- множество работ, которые выполняются на m ма-шинах, причем все работы проходят имеющиеся машины в одной и той же последовательности. Требуется найти такой порядок запуска работ на испол-нение, при котором суммарное время простоя всех машин будет минималь-ным.
Очевидно, что имеется всего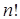 
таких порядков запуска на исполнение, каждый из которых представляет собой перестановку 
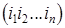номеров работ .
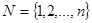Организацию полного перебора вариантов можно, в частности, провести методом ветвей и границ. Перед тем, как описать применение этого метода к поставленной задаче, заметим, что искомая последовательность ра-бот, минимизирующая суммарное время простоя машин, является минимизи-рующей и общее время выполнения всех работ. Ниже мы будем искать эту последовательность работ, как обладающую именно этой последней характе-ристикой: минимальное время выполнения всех работ.
Для большей ясности мы будем далее предполагать, что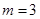 
.
Итак, пусть P - множество всех 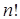последовательностей 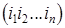. Пусть 
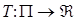- функция, сопоставляющая каждому расписанию 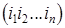время завершения всех работ. Требуется найти минимум этой функции.
|
|
|
Согласно методу ветвей и границ, нужно построить оценочную функ-цию на множестве подмножеств множества P и систему разбиений этого множества, приводящую к рекорду.
Построим три вспомогательные функции на множестве S подмножеств множества P, которые обозначим, соответственно,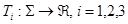 
. Пусть символ 
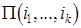обозначает множество всех расписаний, начинающихся с последовательности 
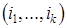. Очевидно, символ 
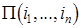обозначает мно-жество, состоящее из единственного элемента 
.
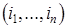Итак, пусть
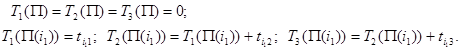
Таким образом,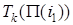 
- время окончания исполнения работы 
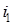на k -ой машине. Далее определим функции 
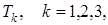рекуррентно:
,
,
.
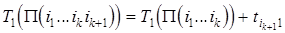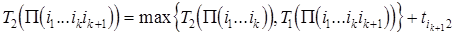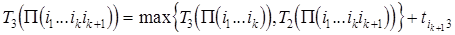Теперь можно построить сразу три оценочных функции для множеств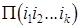 
, которые будем обозначать так: D1, D2 и D3. Вот их определение (мы будем обозначать для удобства записи 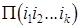через x и через 
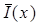те работы из множества 
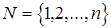, которых нет среди работ 
):
;
;
.
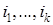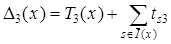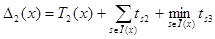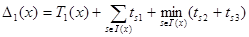Тот факт, что эти функции - оценочные, можно доказать; аналогично, можно доказать то же самое в отношении функции
;
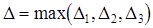она - оценочная.
