Пусть 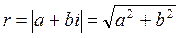
φ – одно из значений аргумента комплексного числа a+bi
Из формул 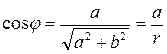 ,
, 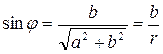
получаем a+bi=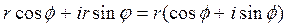
т.о. любое комплексное число можно представить в виде выражения 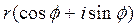 , где r – модуль, φ – одно из значений аргумента.
, где r – модуль, φ – одно из значений аргумента.
Верно и обратное: если комплексное число a+bi представлено в виде
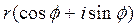 , то
, то 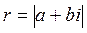 φ=arg(a+bi)
φ=arg(a+bi)
Представление комплексного числа в виде 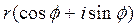 называется
называется
тригонометрической формой комплексного числа.
Действия над комплексными числами:
Дано 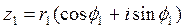
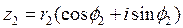
-  *
* =
=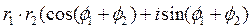 , т.о. при умножении
, т.о. при умножении
двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются;
- 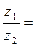
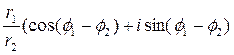 , т.о. при делении
, т.о. при делении
двух комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются;
- 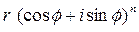
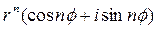 - формула Муавра;
- формула Муавра;
- 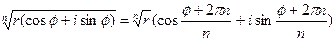 .
.
 2014-02-12
2014-02-12 1252
1252







