Лекция 11
1. Понятие предиката.
2. Логические операции над предикатами.
Главная
1. Понятие предиката
В алгебре логики высказывания рассматриваются как нераздельные целые и только с точки зрения их истинности или ложности. Ни структура высказываний, ни их содержание не затрагиваются. В то же время и в науке, и в практике используются заключения, существенным образом зависящие как от структуры, так и от содержания используемых в них высказываний.
Например, в рассуждении «Всякий ромб - параллелограмм; ABCD - ромб; следовательно, ABCD - параллелограмм» посылки и заключение являются элементарными высказываниями логики высказываний и с точки зрения этой логики рассматриваются как целые, неделимые, без учета их внутренней структуры. Следовательно, алгебра логики, будучи важной частью логики, оказывается недостаточной в анализе многих рассуждений.
В связи с этим возникает необходимость в расширении логики высказываний, в построении такой логической системы, средствами которой можно было бы исследовать и структуру тех высказываний, которые в рамках логики высказываний рассматриваются как элементарные.
Такой логической системой является логика предикатов, содержащая всю логику высказываний в качестве своей части.
Логика предикатов расчленяет элементарное высказывание на субъект (буквально — подлежащее, хотя оно и может играть роль дополнения) и предикат (буквально - сказуемое, хотя оно может играть и роль определения).
Субъект — это то, о чем что-то утверждается в высказывании; предикат - это то, что утверждается о субъекте.
Например, в высказывании «7 - простое число», «7» -субъект, «простое число» - предикат. Это высказывание утверждает, что «7» обладает свойством «быть простым числом».
Если в рассмотренном примере заменить конкретное число 7 переменной х из множества натуральных чисел, то получим высказывательную форму «х - простое число». При одних значенияхх, (например, х = 13, х =17) эта форма дает истинные высказывания, а при других значениях х (например, х = 10, х = 18) эта форма дает ложные высказывания.
Ясно, что эта высказывательная форма определяет функцию одной переменной х, определенной на множестве N, и принимающую значения из множества {1,0}.
Здесь предикат становится функцией субъекта и выражает свойство субъекта.
Определение. Одноместным предикатом Р(х) называется произвольная функция переменного х, определенная на множестве М и принимающая значения из
множества {1,0}.
Множество М, на котором определен предикат P(х), называется областью определения предиката.
Множество всех элементов х Î М, при которых предикат принимает значение «истина», называется множеством истинности предиката Р(х), то есть множество истинности предиката Р(х) - это множество 1р = {х| х Î М, Р(х) = 1}.
Так, предикат -Р(х) - «х - простое число» определен на множестве N, а множество Iр для него есть множество всех простых чисел.
Предикат Q{x} - «sin х = 0» определен на множествеR, а его множество истинности Iq= {x| x = pk; kÎ Z}.
Предикат F(x) - «Диагонали параллелограмма х перпендикулярны» определен на множестве всех параллелограммов, а его множеством истинности является множество всех ромбов.
Приведенные примеры одноместных предикатов выражают свойства предметов.
Рассмотрим примеры предикатов:
Р(х): «х2 + 1> 0, xÎ R»; область определения предиката М= R и область истинности – тоже R, т.к. неравенство верно для всех действительных чисел. Таким образом, для данного предиката М = Ip. Такие предикаты называются тождественно истинными.
В(х): «х2 + 1< 0, xÎ R»; область истинности Ip =Æ, т.к. не существует действительных чисел, для которых выполняется неравенство. Такие предикаты называются тождественно ложными.
Определение. Предикат Р(х), определенный на множестве М, называется тождественно истинным (тождественно ложным), если 1р = М (1р = Æ).
Предикат sin2x+cos2x=1 – тождественно истинный, предикат 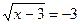 - тождественно ложный.
- тождественно ложный.
Естественным обобщением понятия одноместного предиката является понятие многоместного предиката, с помощью которого выражаются отношения между предметами.
Примером отношения между двумя предметами является отношение «меньше» («больше»). Пусть это отношение введено на множестве Z целых чисел. Оно может быть охарактеризовано высказывательной формой «х < у»(«х > y»), где х, у Î Z, то есть является функцией двух переменных Р(х, у), определенной на множестве Z х Z с множеством значений {1,0}.
Определение. Двухместным предикатом Р(х,у) называется функция двух переменных х и у (субъекты предиката), определенная на множестве М =М1 ´ М2 (хÎ М1, уÎ М2) и принимающая значения из множества {1,0}.
Найдем значения предиката «х < у», где х, у Î Z для пар (2,1), (4,4), (3,7):
Вместо х и у подставим указанные значения: Р(2,1) = 0, т.к. 2>1; Р(4,4)=0, т.к. 4 = 4; Р(3,7)=1, т.к. 3
Рассмотрим этот же предикат, но с областью определения M = R2, тогда область его истинности можно представить графически: это все точки части плоскости (открытая, бесконечная область), лежащей ниже прямой у = х.
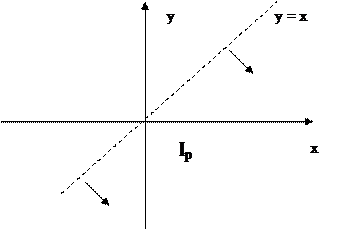 |
В числе примеров двухместных предикатов можно назвать предикаты: Q(х, у): «х = у» -предикат равенства, определенный на множестве М = R х R, область истинности которого – все точки прямой у = х:

Предикат F(x,y): «х//у»- прямая х параллельна прямой у, определенный на множестве прямых, лежащих на данной плоскости.
Аналогично определяется n -местный предикат.
Определение: n – местным предикатом называется функция Q(x1, x2,…,xn), определенная на множестве М = М1´ М2´…´Мn и принимающая на этом множестве значение из множества {1, 0}.
Предикат Р(х) является следствием предиката Q(x) (Q(x)®P(x)), если IQÌIP.
Предикаты P(x) и Q(x) равносильны (Q(x)«P(x)), если IQ=IP.
Для n –местных предикатов вводятся аналогичные понятия.
Примеры:
1. На множестве М= {3,4,5,6,7,8} заданы предикаты P(x): «х – простое число», Q(x): «х – нечетное число». Составить таблицы истинности. Равносильны ли предикаты на множестве а) М; б) L = {2,3,4,5,6,7,8}; в) К = {3,4,5,6,7,8,9}?
Составим таблицы истинности предикатов на данных множествах:
| М | Р(х) | Q(x) | L | Р(х) | Q(x) | K | Р(х) | Q(x) |
На множестве М IP = IQ, следовательно на этом множестве предикаты равносильны. На множествах L и К условие равносильности не соблюдается.
2. Будут ли предикаты равносильны или один из них является следствием другого, если область определения R?
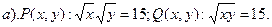
Область допустимых значений х и у для Р(х, у): x>0 и y>0; область истинности – все точки ветви гиперболы у = 15/х, лежащей в первой четверти.
Область допустимых значений х и у для Q(х, у): x>0 и y>0, или x
Значит, IPÌ IQ и предикат Q(x) является следствием предиката Р(х).
б) Р(х): «х2£ 0», Q(x): «2|x| = cosx».
Область истинности предиката Р(х): х =0, область истинности предиката Q(x): х = 0.
Значит, IP = IQ и предикаты равносильны.
 2014-02-12
2014-02-12 1947
1947








