Уравнения, квадратные относительно производной

Такие уравнения имеют вид:

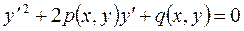, (4.5)

и их можно решить относительно :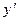

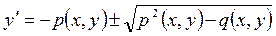. (4.6)

Эти уравнения заданы в области p² – q ³ 0. Интегрируя уравнения (4.6), найдем общий интеграл уравнения (4.5).

Особым решением уравнения (4.5) может быть только дискриминантная кривая:

p² – q = 0,

получающаяся исключением 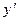из системы:

.

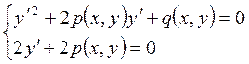Пример 4.1. Найти общий интеграл уравнения:

.

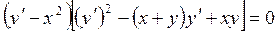▲ Решая исходное уравнение относительно 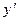, получим

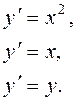
Решая каждое из этих уравнений в отдельности, получаем их общие интегралы:

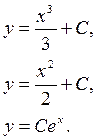
Следовательно, общий интеграл исходного уравнения будет иметь вид:

.▲

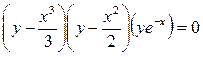Пример 4.2. Найти общий интеграл уравнения:

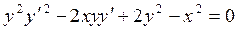
и определить имеет ли это уравнение особое решение.

▲ Решая исходное уравнение относительно 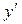, получим

.

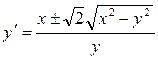Интегрируя это уравнение, найдем

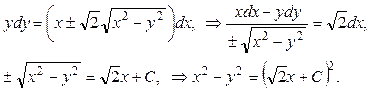
Откуда получаем общий интеграл: .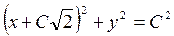

Он представляет собой семейство окружностей с центрами в точках 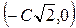и радиусом равным С.

Особым решением может быть только дискриминантная кривая 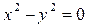, которая распадается на прямые у = х и у = -х.

Полупрямые у = ± х, х ¹ 0 будут особыми решениями. Они являются огибающими семейства окружностей. ▲