Уравнение (4.1) имеет вид
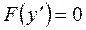 , (4.7)
, (4.7)
причем существует, по крайней мере, один действительный корень 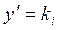 этого уравнения.
этого уравнения.
Так как уравнение (4.7) не содержит х и у, то ki – постоянное. Следовательно, интегрируя уравнение 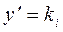 , получим
, получим 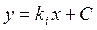 , или
, или 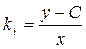 , но ki является корнем уравнения (4.7), следовательно,
, но ki является корнем уравнения (4.7), следовательно,
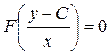 , (4.8)
, (4.8)
является интегралом рассматриваемого уравнения.
Пример 4.3. Записать общий интеграл уравнения:
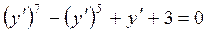 .
.
▲ Так как  , а
, а 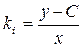 , то общий интеграл исходного уравнения согласно (4.8) будет иметь вид:
, то общий интеграл исходного уравнения согласно (4.8) будет иметь вид:
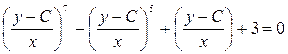 .▲
.▲
Уравнение (4.1) имеет вид
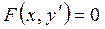 . (4.9)
. (4.9)
Для решения таких уравнений целесообразно ввести параметр t и заменить уравнение (4.9) двумя уравнениями:
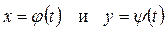 . (4.10)
. (4.10)
Так как 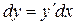 , то в данном случае
, то в данном случае 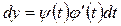 , откуда
, откуда
 , (4.11)
, (4.11)
и, следовательно, интегральные кривые уравнения (4.9) определяются в параметрической форме следующими уравнениями:
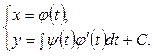 (4.12)
(4.12)
Если уравнение (4.9) легко разрешимо относительно х, 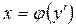 , то почти всегда удобно в качестве параметра ввести
, то почти всегда удобно в качестве параметра ввести 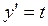 . Тогда интегральные кривые уравнения (4.9) определяются в параметрической форме следующими уравнениями:
. Тогда интегральные кривые уравнения (4.9) определяются в параметрической форме следующими уравнениями:
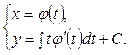 (4.13)
(4.13)
Пример 4.4. Найти решение уравнения: 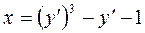 .
.
▲ Введем параметр 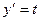 , тогда
, тогда
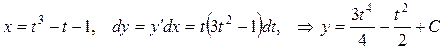 .
.
Следовательно, семейство искомых решений определяют уравнения:
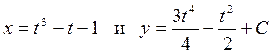 .▲
.▲
Пример 4.5. Записать решение уравнения: 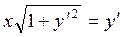 .
.
▲ Для решения этого уравнения необходимо ввести параметр в виде
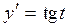 , причем
, причем  ;
;
тогда
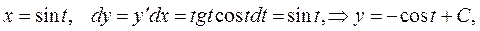
или, исключая параметр t из уравнений
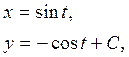
получим 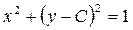 - семейство окружностей. ▲
- семейство окружностей. ▲
Уравнение (4.1) имеет вид
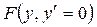 . (4.14)
. (4.14)
Этот вид уравнений, так же как и предыдущий более целесообразно решать, вводя параметр t и заменяя уравнение (4.14) двумя уравнениями (4.10). Так как 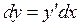 , то
, то  , откуда
, откуда 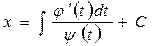 , следовательно, искомые интегральные кривые в параметрической форме определяются уравнениями:
, следовательно, искомые интегральные кривые в параметрической форме определяются уравнениями:
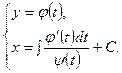 (4.15)
(4.15)
Если уравнение (4.14) легко разрешимо относительно у, то удобно за параметр взять 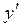 . Действительно, если
. Действительно, если 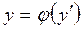 , то, полагая
, то, полагая 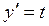 , получим
, получим 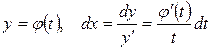 , а искомые интегральные кривые определяются уравнениями:
, а искомые интегральные кривые определяются уравнениями:
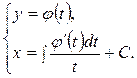 (4.16)
(4.16)
Пример 4.6. Записать решение уравнения:
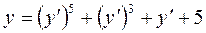 .
.
▲ Для решения этого уравнения необходимо ввести параметр в виде 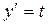 , тогда
, тогда
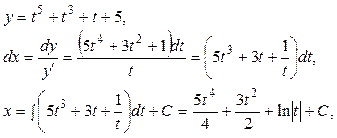
а искомое решение определяется уравнениями:
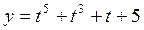 ,
,
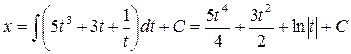 .▲
.▲
Рассмотрим общий случай. Пусть для уравнения (4.1) существую такие функции
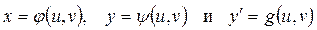 , (4.17)
, (4.17)
что
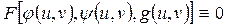 ,
,
относительно параметров u и v из некоторой области их задания. Тогда, используя соотношение  , получаем
, получаем
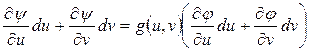 , (4.18)
, (4.18)
откуда
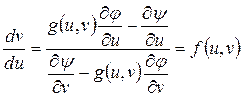 . (4.19)
. (4.19)
Если уравнение (4.19) имеет общее решение 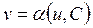 , то общее решение исходного уравнения записывается в параметрической форме
, то общее решение исходного уравнения записывается в параметрической форме
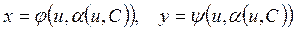 . (4.20)
. (4.20)
Если уравнение (4.1) легко разрешимо относительно у, то за параметры u и v удобно брать х и 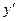 . Действительно, если уравнение (4.1) приводится к виду
. Действительно, если уравнение (4.1) приводится к виду
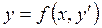 , (4.21)
, (4.21)
то, считая х и 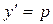 параметрами, получим
параметрами, получим
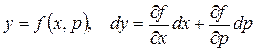 ,
,
или
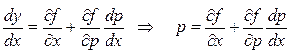 . (4.22)
. (4.22)
Интегрируя уравнение (4.22), получим Ф (х,р,С) = 0. Совокупность уравнений
Ф (х,р,С) = 0 и 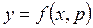 , (4.23)
, (4.23)
где р – параметр, определяет семейство интегральных кривых исходного уравнения.
Если уравнение (4.1) легко разрешается относительно х:
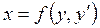 . (4.24)
. (4.24)
то в этом случае взяв за параметры у и 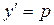 и пользуясь зависимостью
и пользуясь зависимостью 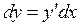 , получим
, получим
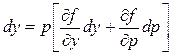
или
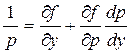 . (4.25)
. (4.25)
Интегрируя уравнение (2.25), получим Ф (у,р,С) = 0, которое совместно с уравнением (4.24) будет определять все решения уравнения (4.1).
Пример 4.7. Найти решения уравнения: 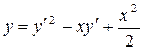 .
.
▲ Это уравнение допускает параметрическое представление
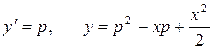 .
.
Пользуясь равенством  , получаем
, получаем 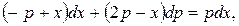 откуда
откуда 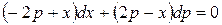 или
или 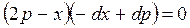 . Это уравнение распадается на два уравнения:
. Это уравнение распадается на два уравнения:
 и 2 р - х = 0.
и 2 р - х = 0.
Первое из них дает р = х + С. Подставляя это значение р в выражение для у, получаем
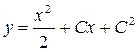 .
.
Это общее решение исходного уравнения.
Из второго уравнения 2 р – х = 0 находим р = х/ 2. Подставляя это значение р также в выражение для у, получаем 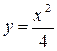 . Это также решение исходного уравнения и притом особое. ▲
. Это также решение исходного уравнения и притом особое. ▲
Пример 4.8. Найти решения уравнения: 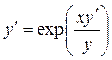 .
.
▲ Разрешив это уравнение относительно х и, полагая в этом уравнении 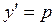 , получим
, получим 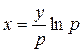 . Так как
. Так как 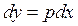 , то
, то
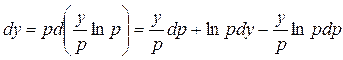 ,
,
или
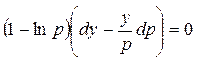 .
.
Из этого уравнения находим: р = е и 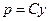 . Таким образом, решения исходного уравнения имеют вид:
. Таким образом, решения исходного уравнения имеют вид:
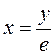 и
и 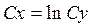 .▲
.▲
 2014-02-12
2014-02-12 821
821








