2014-02-12
1350
Рассмотрим уравнение вида
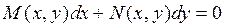, (3.1)
которое будет называться уравнением в полных дифференциалах, если существует такая функция u=u (x,y), что ее полный дифференциал совпадает с левой часть уравнения (3.1), т.е.
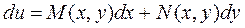. (3.2)
С другой стороны полный дифференциал функции u=u (x,y) равен
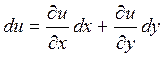, (3.3)
поэтому из выражений (3.2) и (3.3) следует выполнение тождеств
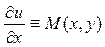и 
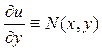(3.4)
Необходимым и достаточным условием существования функции u=u(x,y) (при существовании непрерывных частных производных первого порядка от функций М(х,у) и N(x,y)), является выполнение тождества
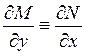, (3.5)
которое называется условием Эйлера.
Если же условие (3.5) выполняется, то функция u=u(x,y) определяется по формуле:
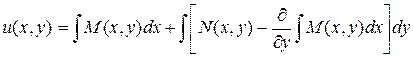, (3.6)
или же в виде:
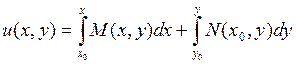. (3.7)
В этой формуле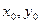 
можно брать произвольно, лишь бы точка 
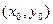оставалась в области где М(х,у) и N(x,y) и их частные производные были бы непрерывны.
Итак, если левая часть уравнения (3.1) совпадает с полным дифференциалом функции u=u(x,y), то справедливо выражение
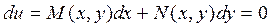или du = 0. (3.8)
Следовательно, функция u=u(x,y) является общим интегралом уравнения (3.1), т.е
u(x,y) = C, (3.9)
а с учетом (3.6) общий интеграл уравнения (3.1) можно вычислить по формуле
С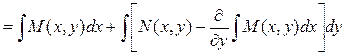
, (3.10)
или с учетом (3.7), по формуле
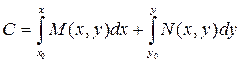. (3.11)
Общий интеграл уравнения (3.1) можно также найти, используя равенства (3.4). Для этого сначала потребуем, чтобы выполнялось равенство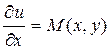 
, отсюда найдем функцию u(x,y):
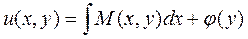, (3.12)
где j (y) – произвольная дифференцируемая функция от у, а при выполнении интегрирования переменную у под знаком интеграла надо считать постоянной.
Теперь из множества функций u(x,y) выделим ту, которая удовлетворяет условию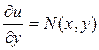 
. Функция u(x,y,) определяемая из (3.12), будет удовлетворять этому условию, если будет выполняться равенство
,
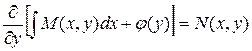или
,
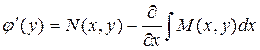то есть функция j(y) должна иметь вид:
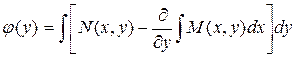. (3.13)
Подставив (3.13) в равенство (3.12), получим искомую функцию u(x,y), а, следовательно, и общий интеграл уравнения (3.1):
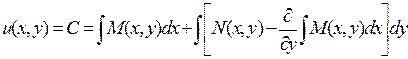. (3.14)
Для получения формулы (3.14) мы потребовали, чтобы выполнялось равенство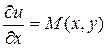 
. Однако, можно потребовать, чтобы в первую очередь выполнялось равенство 
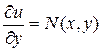и, проводя аналогичные рассуждения, придем к уравнению
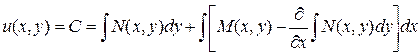, (3.15)
которое так же, как и уравнение (3.14) определяет общий интеграл уравнения (3.1).
Пример 3.1. Найти общий интеграл уравнения:
.
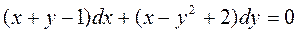▲ Установим, является ли исходное равнение уравнением в полных дифференциалах. Для этого проверим, выполняется ли условие Эйлера (3.5). Здесь
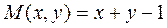, а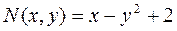 
.
Вычислим производные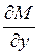 
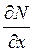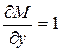и 
: 
и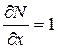 
, следовательно, условие Эйлера выполнено, и исходное уравнение является уравнением в полных дифференциалах. Найдем функцию u(x,y) по изложенной выше схеме, а именно, предположим, чтобы выполнялось равенство 
:
,
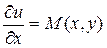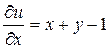отсюда
.
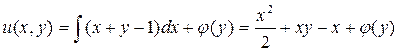Далее потребуем от u(x,y) обеспечения равенства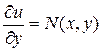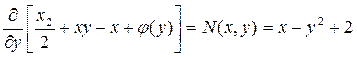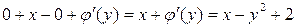 
:
,
или 
, или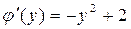 
. Следовательно, 
.
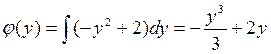Таким образом, искомая функция и соответственно общий интеграл исходного уравнения будут иметь вид:
.
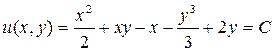Получим общий интеграл исходного уравнения, потребовав выполнения равенства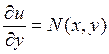 
:
,
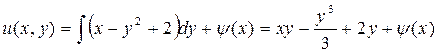а теперь потребуем, чтобы выполнялось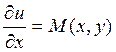 
: 
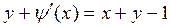. Найдем 
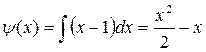. Таким образом, общий интеграл исходного уравнения имеет вид:
.
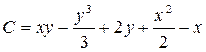Следовательно, независимо от того, какое из условий (3.4) будет выполняться в первую очередь, общий интеграл исходного уравнения будет одним и тем же.
Общий интеграл исходного уравнения можно записать в виде (3.11):
.
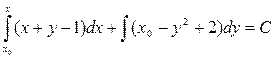Выполним интегрирование:
,
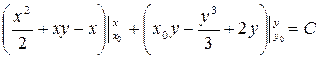или
,
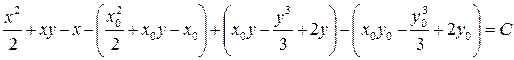т.к.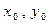 
можно брать произвольно, то, обозначив 
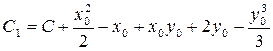, окончательно получим
.▲
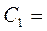
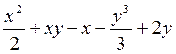2. Если мы вновь обратимся к уравнению (3.1):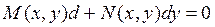 
, то можем отметить, что для него не всегда выполняется условие Эйлера (3.5):
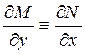
Несмотря на этот факт, в некоторых случаях удается достаточно просто подобрать некую функцию m(x,y) так, чтобы после умножения на нее левая часть уравнения (3.1) обращается в полный дифференциал, т.е. уравнение
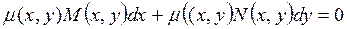
уже является уравнением в полных дифференциалах и выполняется тождество:
.
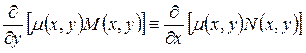Такая функция m(x,y) называется интегрирующим множителем для данного уравнения и определяется из уравнения
,
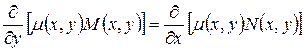которое можно переписать в виде:
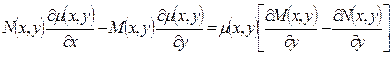. (3.16)
Если заранее известно, что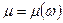 
, где w -заданная функция от х и у, то уравнение (3.16) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией m от независимой переменной w:
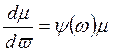, (3.17)
где -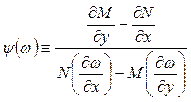 
(3.18)
т.е. дробь справа является функцией только от w.
Решая уравнение (3.17), находим интегрирующий множитель
.
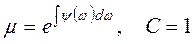В частности, уравнение (3.1) будет иметь интегрирующий множитель, зависящий только от х (w = х) или только от у (w = у), если выполнены соответствующие условия:
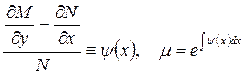, (3.19)
или
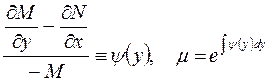. (3.20)
Пример 3.2. Найти общий интеграл уравнения:
.
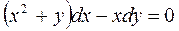▲ Определим, является ли это уравнение уравнением в полных дифференциалах. Проверим, выполняется ли условие Эйлера. Для этого вычислим частные производные от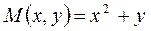 
по у, и от 
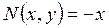по х:
,
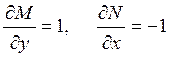следовательно, условие Эйлера не выполнено и исходное уравнение не является уравнением в полных дифференциалах.
Проверим, существует ли для этого уравнения интегрирующий множитель, зависящий только от х? Для этого проверим условие (3.19):
.
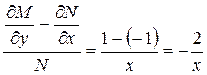Следовательно, ответ на поставленный вопрос положителен, и можно определить интегрирующий множитель:
.
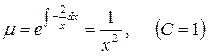Таким образом, умножив исходное уравнение на этот множитель, мы приведем его к уравнению в полных дифференциалах:
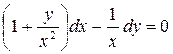. (П3.1)
Проверив еще раз условие Эйлера, установим:
.
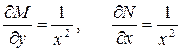Результат проверки свидетельствует о том, что полученное уравнение (П3.1) является уравнением в полных дифференциалах. Найдем общий интеграл уравнения (П3.1).
,
.
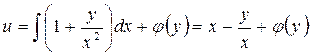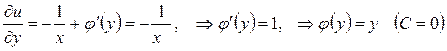Таким образом, общий интеграл исходного уравнения имеет вид:
.▲
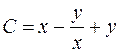Пример 3.3. Найти общий интеграл уравнения:
.
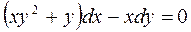▲ Это уравнение не является уравнением в полных дифференциалах, т.к.
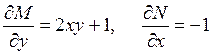
Проверим, имеет ли это уравнение интегрирующий множитель зависящий только от у: m = m(у).
Действительно, проверим условие (3.20):
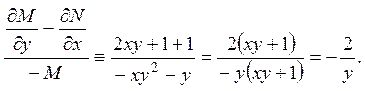
Следовательно,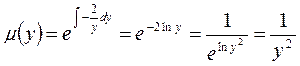 
.
После умножения исходного уравнения на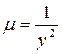 
, получим уравнение
,
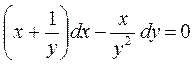которое будет являться уравнением в полных дифференциалах, т.к.
.
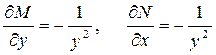Следовательно, интегрируя последнее уравнение, будем иметь:
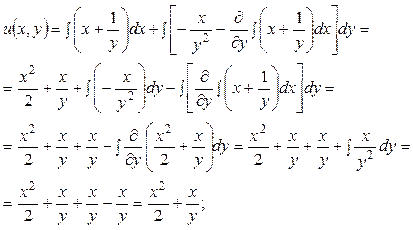
Таким образом, общий интеграл исходного уравнения будет иметь вид:
.▲
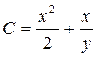Пример 3.4. Найти общий интеграл уравнения:
.
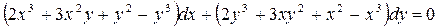▲ Проверка условия Эйлера для этого уравнения показала, что оно не выполняется:
.
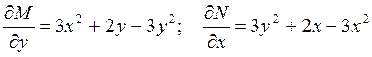Достаточно просто убедиться о том, что это уравнение не имеет интегрирующих множителей, зависящих только от х и только от у:
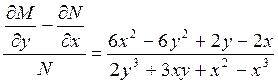
и
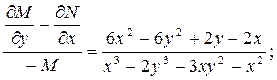
В этом случае предположим, что w в (3.19) равно: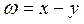 
. Тогда 
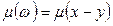и уравнение (3.19) с учетом (3.20) принимает вид:
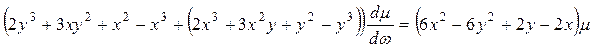или
.
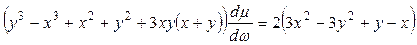Очевидно, что выражение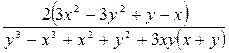 
не является функцией от 
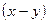, поэтому будем искать функцию m в виде 
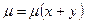. Тогда, аналогично проведенному выше, имеем
,
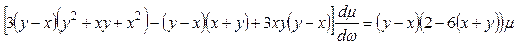откуда окончательно находим
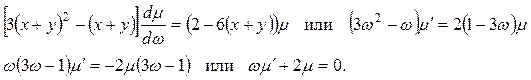
Решая последнее уравнение, находим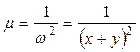 
. Умножив исходное уравнение на 
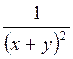, приведем исходное уравнение к уравнению в полных дифференциалах. Его общий интеграл имеет вид:
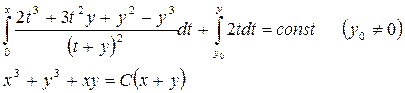
Отметим, что решение у = -х содержится в общем интеграле при С = ∞.▲
Пример 3.5. Найти общий интеграл уравнения:
.
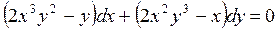▲ Это уравнение не является уравнением в полных дифференциалах. Найдем интегрирующий множитель, с помощью которого можно привести исходное уравнение к уравнению в полных дифференциалах.
Пусть w = xy. Тогда согласно (3.19) будем иметь
.
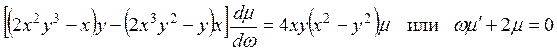Отсюда находим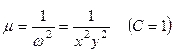 
. Исходное уравнение приводится к уравнению в полных дифференциалах:
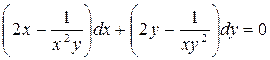
Найдем общий интеграл уравнения
▲
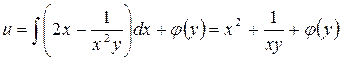
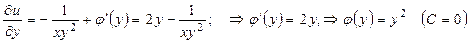
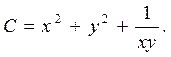Пример 3.6. Проинтегрировать уравнение:
,
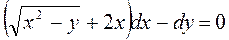если известно, что для того, чтобы привести исходное уравнение к уравнению в полных дифференциалах необходимо использовать интегрирующий множитель вида: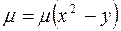 
.
▲ Полагаем в условии (3.20)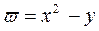 
:
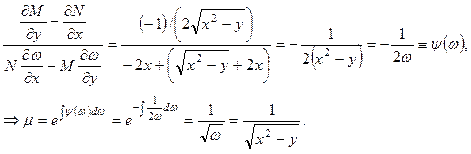
Умножая исходное уравнение на этот интегрирующий множитель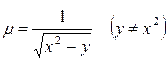 
, мы приведем исходное уравнение к уравнению в полных дифференциалах:
.
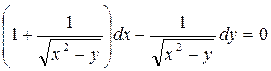Решая это уравнение, найдем общий интеграл исходного уравнения:
.
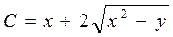При умножении исходного уравнения мы предполагали, что у ¹ х 2, т.к., если у = х 2, то m обращается в бесконечность. Поэтому у = х 2 также будет являться решением. ▲
