Уравнение вида
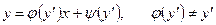 , (4.26)
, (4.26)
в котором у является линейной функцией от х с коэффициентами, зависящими от 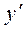 , причем коэффициент при х не равен
, причем коэффициент при х не равен 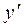 , называется уравнением Лагранжа. Построение его общего решения в параметрической форме сводится к интегрированию линейного уравнения.
, называется уравнением Лагранжа. Построение его общего решения в параметрической форме сводится к интегрированию линейного уравнения.
Положим 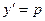 , где р – параметр, тогда уравнение (4.26) принимает вид:
, где р – параметр, тогда уравнение (4.26) принимает вид:
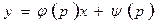 . (4.27)
. (4.27)
Заменив в равенстве 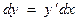 величину dy ее значением из (4.27), а вместо
величину dy ее значением из (4.27), а вместо 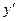 подставим р:
подставим р:
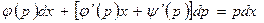
или
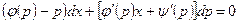 . (4.28)
. (4.28)
Уравнение (4.28) можно привести к линейному уравнению с искомой функцией х, если разделить обе его части на dp и 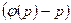 . После выполнения этих действий, получим
. После выполнения этих действий, получим
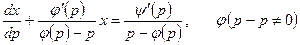 . (4.29)
. (4.29)
Поскольку уравнение (2.29) линейно относительно х и 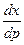 и, следовательно, легко интегрируется, например методом вариации произвольной постоянной. Получив интеграл Ф (х,р,С) = 0 уравнения (4.29) и присоединяя к нему уравнение (4.27), получим
и, следовательно, легко интегрируется, например методом вариации произвольной постоянной. Получив интеграл Ф (х,р,С) = 0 уравнения (4.29) и присоединяя к нему уравнение (4.27), получим
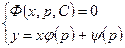 . (4.30)
. (4.30)
Эти уравнения определяют искомые интегральные кривые.
При переходе от уравнения (4.28) к уравнению (4.29) пришлось делить на 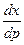 . Но при этом мы потеряли решения, если они существуют, для которых р постоянно, а значит
. Но при этом мы потеряли решения, если они существуют, для которых р постоянно, а значит 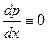 . Считая р постоянным, замечаем, что уравнение (4.28) удовлетворяется лишь в том случае, когда р является корнем уравнения
. Считая р постоянным, замечаем, что уравнение (4.28) удовлетворяется лишь в том случае, когда р является корнем уравнения
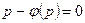 . (4.31)
. (4.31)
Итак, если уравнение (4.31) имеет действительные корни 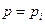 , то к найденным выше решениям уравнения Лагранжа надо добавить еще
, то к найденным выше решениям уравнения Лагранжа надо добавить еще
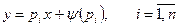 . (4.32)
. (4.32)
Эти прямые линии могут оказаться особыми решениями уравнения Лагранжа.
Пример 4.9. Найти решения уравнения: 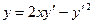 .
.
▲ Полагая в этом уравнении 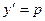 , будем иметь
, будем иметь
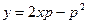 .
.
Дифференцируя обе части этого уравнения по р, получим
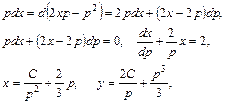
подставляя р = 0 в равенство 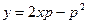 , находим у = 0.Это также является решением исходного уравнения, и притом частное. ▲
, находим у = 0.Это также является решением исходного уравнения, и притом частное. ▲
Пример 4.10. Найти решения уравнения: 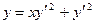 .
.
▲ Полагая в этом уравнении 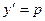 , будем иметь
, будем иметь
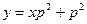 или
или 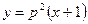 . (П4.10.1)
. (П4.10.1)
Продифференцируем это равенство:
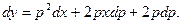
Производя замену 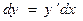 , приходим к уравнению:
, приходим к уравнению:
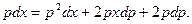
Отсюда, сокращая на р, получаем уравнение с разделяющимися переменными:
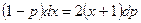 или
или 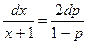 .
.
Интегрируя это уравнение, получим:
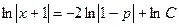 или
или 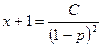 .
.
Подставив это уравнение в (П4.10.1), получим: 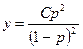 .
.
При сокращении на р мы потеряли особое решение; полагая р = 0, находим из данного уравнения у = 0: это и есть особое решение.
Следовательно,
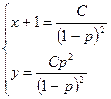 - общее решение исходного уравнения,
- общее решение исходного уравнения,
а у = 0 – особое решение.
В общем решении параметр р можно исключить и привести его к виду:
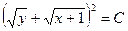 .▲
.▲
 2014-02-12
2014-02-12 702
702








