Основные понятия и определения. Задачи для самостоятельной работы

Лекция 4. УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, НЕРАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ

Задачи для самостоятельной работы

Найти общий интеграл уравнений.

3.1. 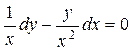. 3.2. .

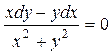3.3. .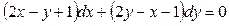

Решить задачу Коши

3.4. .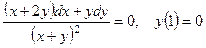

3.5. .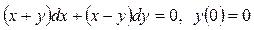

3.6. .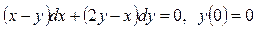

Проинтегрировать уравнения с помощью интегрирующего множителя.

3.7. 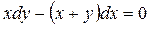. 3.8. .

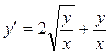Решить уравнения с помощью интегрирующих множителей одного из видов:

.

3.9. , .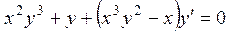

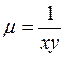3.10. , .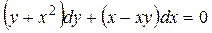

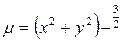Дифференциальное уравнение первого порядка, не разрешенное относительно производной, имеет вид:

. (4.1)

Решение этого уравнения может быть представлено как в явном виде: , так и в неявном виде: 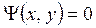, и параметрическом виде: .

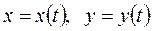Для уравнений (4.1) так же, как и для уравнений, разрешенных относительно производной, может ставиться задача Коши и имеет место единственность ее решения. Решение уравнения (4.1) будет частным решением, если в каждой точке его сохраняется единственность решения задачи Коши. Если же в каждой точке решения нарушается единственность решения задачи Коши, то оно будет особым решением.

Кривую подозрительную на особое решение при условии, что левая часть уравнения (4.1) непрерывна по совокупности переменных и имеет частную производную по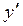, можно найти путем исключения 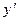из системы:

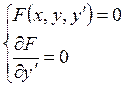. (4.2)

Эта кривая называется дискриминантной кривой уравнения (4.1) и для того, чтобы она была особым решением этого уравнения необходимо, чтобы она была его решением и в каждой ее точке нарушалась единственность решения задачи Коши.