Уравнение вида
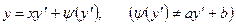 , (4.33)
, (4.33)
называется уравнением Клеро. Оно отличается от уравнения Лагранжа только тем, что в нем коэффициент при х равен 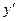 .
.
Полагая 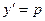 , где р – параметр, получим:
, где р – параметр, получим:
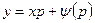 . (4.34)
. (4.34)
Дифференцируя по х, будем иметь:
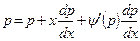 или
или 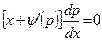 , (4.35)
, (4.35)
откуда
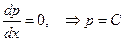 ,
,
или
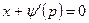 .
.
В первом случае, исключая р, получим
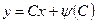 (4.36)
(4.36)
- однопараметрическое семейство интегральных кривых.
Во втором случае решение определяется уравнениями
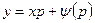 и
и 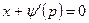 . (4.37)
. (4.37)
Нетрудно проверить, что интегральная кривая, определяемая уравнениями (4.37), является огибающей семейства прямых (4.36).
Действительно, огибающая некоторого семейства Ф (х,у,С) = 0 определяется уравнениями
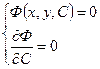 , (4.38)
, (4.38)
которые для семейства (4.36) имеют вид
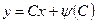 ,
, 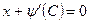 ,
,
и лишь обозначением параметра отличаются от уравнений (4.37).
Пример 4.11. Найти решения уравнения: 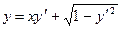 .
.
▲ Это уравнение Клеро. Полагая в этом уравнении 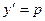 ,
, 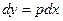 будем иметь:
будем иметь:
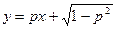 . (П4.11.1)
. (П4.11.1)
Отсюда:
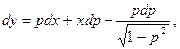
или 
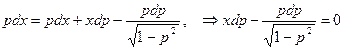 .
.
Наконец,
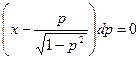 . (П4.11.2)
. (П4.11.2)
Это уравнение может выполняться для функций двух видов:
1. Для таких функций у (х), для которых dp = 0, т.е. функций вида:
у =Сх+С1.
Но не все линейные функции этого вида удовлетворяют данному уравнению, а лишь те, которые имеют вид:
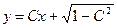 . (П4.12.3)
. (П4.12.3)
Это есть общий интеграл исходного уравнения Клеро (он получается из уравнения (П4.11.1) простой заменой 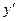 на С).
на С).
2. Уравнение (П4.11.2) выполняется и для таких функций у (х), для которых выполняется тождество
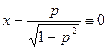 .
.
Присоединяя это уравнение к уравнению (П4.11.1), мы также получаем решение исходного уравнения:
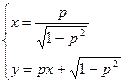 ,
,
которое будет особым решением.
Исключение р из этой системы, приводит к уравнению:
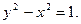
Если общее решение (П4.11.3) выражает однопараметрическое семейство прямых, то особое решение выражает равнобочную гиперболу. Эта гипербола служит огибающей семейства прямых (П4.11.3).▲
Пример 4.12. Найти решения уравнения: 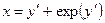 .
.
▲Введем параметр, обозначая 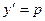 , тогда исходное уравнение будет иметь вид:
, тогда исходное уравнение будет иметь вид:
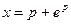 . (П4.12.1)
. (П4.12.1)
Выразим у через р для чего из последнего равенства выразим dx, используя равенство 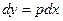 :
:
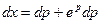 .
.
Следовательно,
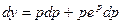 .
.
Интегрируя последнее уравнение, получим
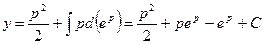 . (П4.12.2)
. (П4.12.2)
Равенства (П4.12.1) и (П4.12.2) совместно выражают в параметрической форме общее решение исходного уравнения Клеро:
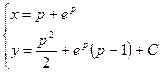 . ▲
. ▲
Пример 4.13. При детальном изучении поверхности выработки необходимо сфокусировать световое излучение таким образом, чтобы освещенность поверхности была максимальной. Для этого необходимо определить меридиан поверхности вращения зеркала, обеспечивающий фокусировку световых лучей, падающих на его поверхность параллельно оси вращения, которые после отражения сходились бы в одной точке на оси вращения.
▲ Пусть фокус будет началом принятой нами системы координат (рис. 4.1).
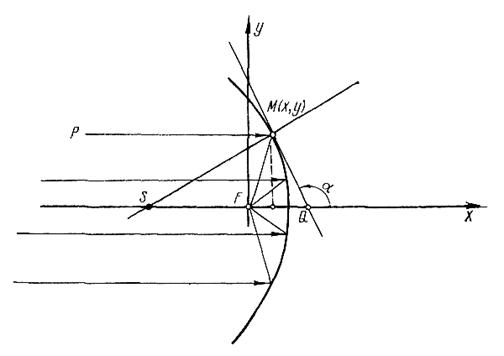
Рис. 4.1
Луч Р падает в точку М поверхности зеркала и, отразившись, проходит через фокус F. В точке М проводим касательную, пересекающую ось абсцисс в точке Q, и нормаль, пересекающую ось абсцисс в точке S.
Пусть α — угол между касательной и положительным направлением оси абсцисс.
Тогда
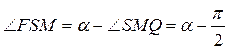
так как внешний угол треугольника равен сумме внутренних неприлегающих углов. Далее
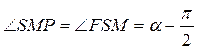
так как это накрест лежащие углы, образуемые пересечением прямой параллельных линий;
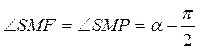
на основании теоремы об углах падения и отражения лучей;
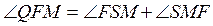
так как внешний угол треугольника равен сумме внутренних неприлегающих углов, или
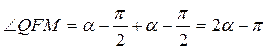
Обозначая координаты точки М через х и у, имеем:
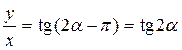
Как известно,
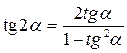
но, с другой стороны,
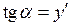 .
.
Поэтому
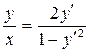
или
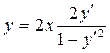 (4.13.1)
(4.13.1)
Это уравнение Лагранжа. Введем параметр следующим образом
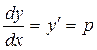 ,
,
Тогда уравнение (4.13.1) можно записать в виде
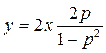 (4.13.2)
(4.13.2)
Таким образом, функция у является функцией двух переменных
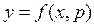
Вычислим полный дифференциал этой функции
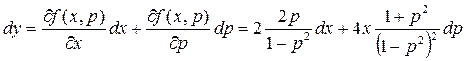
Разделив полученное выражение на dx
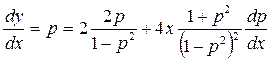 ,
,
Получим уравнение
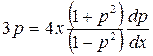 ,
,
разделяя в нем переменные, получим
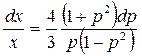 . (4.13.3)
. (4.13.3)
Проинтегрируем уравнение (4.13.3)
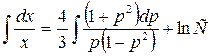 . (4.13.4)
. (4.13.4)
Преобразуем интеграл в правой части равенства (4.13.4):
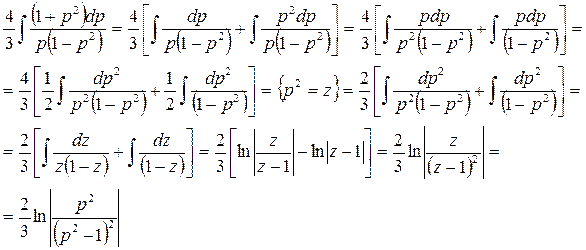
Таким образом, решение уравнения (4.13.4) принимает вид
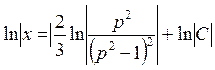
или
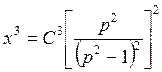
Применяем подстановку
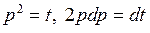 .
.
Тогда
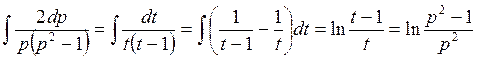 .
.
Подставляя полученное значение в равенство (4.13.2), после интегрирования, полагая С = -ln а, имеем
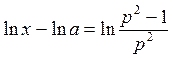 ,
,
откуда
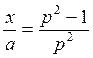
и
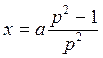 (4.13.3) Из уравнения (4.13.1) получаем
(4.13.3) Из уравнения (4.13.1) получаем
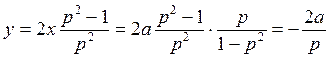
или
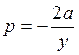
Это выражение подставляем в уравнение (4.13.3):
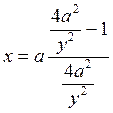
отсюда
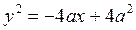 .
.
Итак, меридиан описывается уравнением параболы, симметричной относительно оси абсцисс. ▲
 2014-02-12
2014-02-12 2771
2771
