1. Записать характеристическое уравнение (5.8).
2. Найти корни характеристического уравнения.
3. Пользуясь правилами 1-3, выписать общее решение уравнения в зависимости от типа корней.
Всякое решение линейного уравнения является частным решением и особых решений оно не имеет.
Пример 5.1. Найти общее решение уравнения: 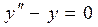 .
.
▲ 1. Запишем характеристическое уравнение: 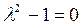 .
.
2. Найдем корни этого уравнения: 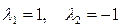 .
.
3. Поскольку корни действительные и различные, то по правилу 1 им ставятся в соответствие функции 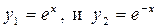 , которые составляют фундаментальную систему линейно независимых решений исходного уравнения. Следовательно, общее решение исходного уравнения имеет вид:
, которые составляют фундаментальную систему линейно независимых решений исходного уравнения. Следовательно, общее решение исходного уравнения имеет вид:
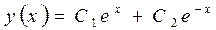 .▲
.▲
Пример 5.2. Найти общее решение уравнения:
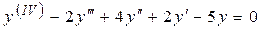 .
.
▲ 1. Запишем характеристическое уравнение:
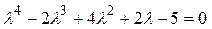 .
.
После преобразований это уравнение можно привести к виду:

2. Найдем корни этого уравнения: 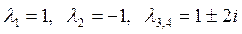 .
.
3. Мы видим, что среди корней характеристического уравнения есть как действительные и различные корни, так и комплексно сопряженные. Поэтому для составления фундаментальной системы линейно независимых решений воспользуемся правилами 1 и 2:
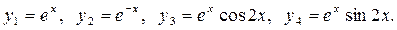
Следовательно, общее решение исходного уравнения имеет вид:
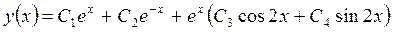 .
.
В пункте 3 нашего решения мы утверждали, что наша фундаментальная система состоит из линейно независимых решений. Проверим, соответствует ли это утверждение действительности.
Проведем доказательство того, что наши частные решения 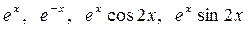 являются линейно независимыми в любом интервале изменения х, от противного, положим, что выполняется тождество:
являются линейно независимыми в любом интервале изменения х, от противного, положим, что выполняется тождество:
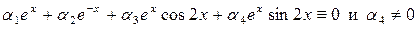 .
.
Разделим это тождество на ех:
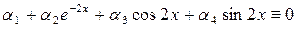 ,
,
дифференцируем:
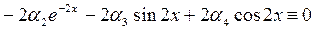 .
.
Делим на e -2 x:
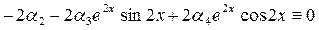 ,
,
и еще раз дифференцируем:
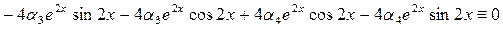 .
.
Делим полученное тождество на  :
:
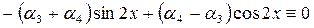 .
.
Это тождество может выполняться только при условии:
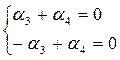
Отсюда вытекает, что 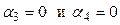 , а это противоречит нашему предположению, что
, а это противоречит нашему предположению, что 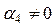 . Следовательно, решения, составляющие фундаментальную систему, являются линейно независимыми. ▲
. Следовательно, решения, составляющие фундаментальную систему, являются линейно независимыми. ▲
Пример 5.3. Найти общее решение уравнения:
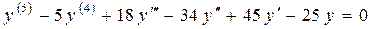 .
.
▲ 1. Запишем характеристическое уравнение:
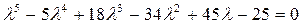 .
.
2. Это характеристическое уравнение имеет корни:
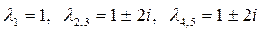 .
.
3. Мы видим, что среди корней характеристического уравнения есть как действительные и различные корни, так и комплексно сопряженные, причем комплексные корни являются кратными. Поэтому для составления фундаментальной системы линейно независимых решений воспользуемся правилами 1, 2 и 3. Корню 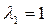 соответствует решение
соответствует решение 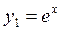 , а каждому из двукратных корней
, а каждому из двукратных корней 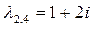 и
и  , отвечают решения:
, отвечают решения: 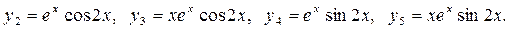 Совокупность этих пяти решений
Совокупность этих пяти решений  - образует фундаментальную систему линейно независимых решений. Следовательно, общее решение запишется так:
- образует фундаментальную систему линейно независимых решений. Следовательно, общее решение запишется так:
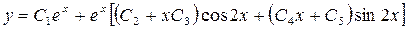 .▲
.▲
 2014-02-12
2014-02-12 1025
1025
