Рассмотрим уравнение второго порядка вида
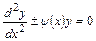 .
.
Такое уравнение можно путем замены независимой переменной вида
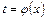
можно привести к виду
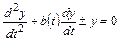 ,
,
а затем с помощью замены
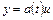 ,
,
в последнем уравнении можно избавится от первой производной. Такое преобразование называется преобразованием Лиувилля.
Уравнение вида
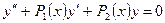
иногда можно свести к уравнению с постоянными коэффициентами с помощью замены
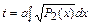 .
.
Дифференциальное уравнение второго порядка с переменными коэффициентами с помощью определенной замены искомой функции можно привести к виду, не содержащему первой производной. Например, уравнение вида
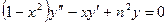 ,
,
которое называется уравнением Чебышева, приводится к однородному линейному уравнению, не содержащему первой производной путем замены аргумента х по формуле 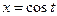 , а именно к уравнению вида:
, а именно к уравнению вида:
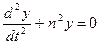 ,
,
общее решение которого имеет вид
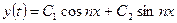 .
.
Исходя из этого, общее решение уравнения Чебышева будет выглядеть так:
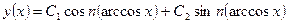 .
.
Пример 6.8. Решить уравнение: 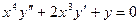 .
.
▲ Для начала, положим 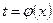 , и подберем функцию
, и подберем функцию 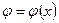 так, чтобы после замены в полученном уравнении отсутствовал член с первой производной. Тогда вычислив производные
так, чтобы после замены в полученном уравнении отсутствовал член с первой производной. Тогда вычислив производные
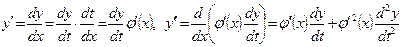 ,
,
и подставив их в исходное уравнение, получим
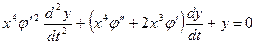 . (П6.8.1)
. (П6.8.1)
Для того, чтобы выполнялось поставленное условие, а именно, в этом уравнении отсутствовал член с первой производной необходимо, чтобы
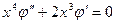 ,
,
откуда определим
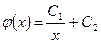 .
.
Подставив эту функцию в уравнение (П6.8.1), получим уравнение:
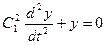 .
.
Это однородное линейное уравнение с постоянными коэффициентами. Составим характеристическое уравнение 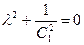 и найдем его корни:
и найдем его корни: 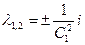 . Следовательно, общее решение будет иметь вид:
. Следовательно, общее решение будет иметь вид:
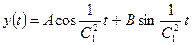 ,
,
а так как в силу нашего предположения о том, что t = 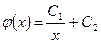 , то решение исходного уравнения будет иметь вид:
, то решение исходного уравнения будет иметь вид:
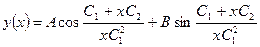 .▲
.▲
 2014-02-12
2014-02-12 1687
1687
