Задания для самостоятельной работы
Исследовать, являются ли данные решения линейно независимыми.
5.1. 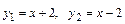 . 5.2.
. 5.2. 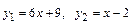 .
.
5.3. 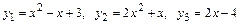 .
.
5.4. 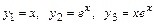 . 5.5.
. 5.5. 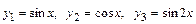 .
.
Найти общие решения однородных уравнений, а также частные решения в тех заданиях, где поставлены начальные условия.
5.6. 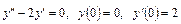 . 5.7.
. 5.7. 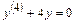 . 5.8.
. 5.8.  .
.
5.9. 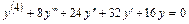 .
.
5.10. 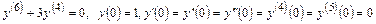 .
.
Найти общие решения неоднородных уравнений, а также частные решения в тех заданиях, где поставлены начальные условия.
5.11. 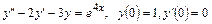 . 5.12.
. 5.12. 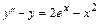 .
.
5.13. 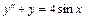 . 5.14.
. 5.14. 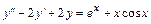 .
.
5.15. 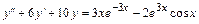 . 5.16.
. 5.16. 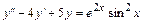 .
.
5.17. 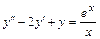 . 5.18.
. 5.18. 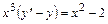 .
.
5.19. 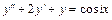 . 5.20.
. 5.20. 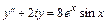 .
.
По заданным корням характеристического уравнения и виду правой части выписать вид частного решения дифференциального уравнения.
5.21. 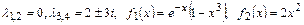 .
.
5.22. 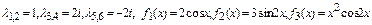 .
.
5.23. 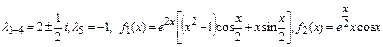 .
.
5.24. 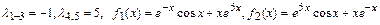 .
.
Решить задачу Коши
5.25. 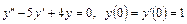 . 5.26.
. 5.26. 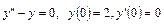 .
.
5.27. 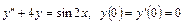 .
.
5.28. 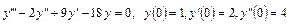 .
.
5.29. 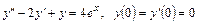 .
.
5.30. 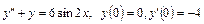 .
.
5.31. При размыкании цепи (в момент появления искры) сопротивление цепи R быстро возрастает от первоначальной величины Ro до бесконечности. На основании опыта допускают, что зависимость R от t в этом процессе выражается
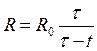
где τ — время всего процесса размыкания. Найти силу тока i в любой момент в цепи при постоянной электродвижущей силе Е и самоиндукции L.
Для выявления и описания основных закономерностей в протекании технологических процессов, связанных с вибрационным перемещением кусков горной массы можно ограничиться рассмотрением модели относительного движения твердого тела вдоль вибрирующей поверхности (лотка), представленной на рис.5.1.
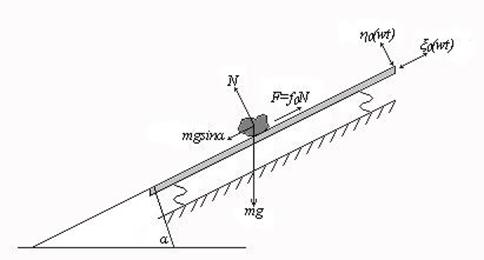
Рис. 5.1. Модель относительного движения твердого тела вдоль вибрирующего лотка
Лоток представляет собой прямолинейное одномерное абсолютно твердое тело, расположенное на упругих опорах, обеспечивающих плоскопараллельное движение лотка относительно жестко неподвижного основания. Продольная ось лотка параллельна основанию и образует с горизонталью некоторый угол α. Предположим, что на лотке лежит кусок массой т, при этом угол α не превышает предельный угол трения скольжения куска, так что он не может самостоятельно, без какого либо внешнего воздействия скользить по лотку.
В определенный момент времени лоток начинает совершать плоские поступательные периодические колебания по закону ξ0(wt) и η0(wt). В зависимости от параметров колебаний лотка возможны различные состояния частицы и режимы ее относительного движения.
Во многих случаях эта простейшая модель позволяет вполне удовлетворительно не только в качественном, но и в количественном отношении решать различные задачи вибрационной технологии (в частности, вибротранспортирования и вибровнедрения).
Движение лотка и материальной частицы будем рассматривать относительно неподвижной системы ортогональных осей координат ξOη причем ось Oξ параллельна продольной оси лотка (рис. 5.1).
Между частицей и лотком возникает нормальная сила N=N(wt), модуль которой зависит от поперечной составляющей вибрации лотка, и тангенциальная сила сухого трения F, направленная против скорости относительного движения ξ-ξ0.
Абсолютное движение частицы в проекциях на неподвижные оси Oη и Oξ можно записать в виде:
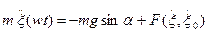 ;
; 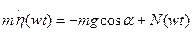 . (5п.1)
. (5п.1)
В зависимости от направления относительной скорости сила трения
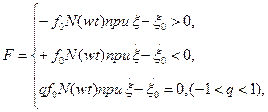 (5п.2)
(5п.2)
где f0 - коэффициент сухого трения; здесь предполагается равенство коэффициентов трения покоя и трения скольжения.
В общем случае направление силы трения удобнее учитывать с помощью signum-функции (при х>0 у=+1; при х < 0 у = -1; при х = 0 -1 < у < +1). Тогда вместо выражений (5п.2), сила трения запишется в виде:
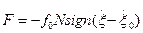 (5п.3)
(5п.3)
Так как основной практический интерес представляет исследование движения частицы относительно вибрирующего лотка, то решение этой задачи целесообразно рассматривать не в абсолютной, а в подвижной системе координат хО1у жестко связанной с лотком и параллельной системе координат ξOη (рис. 5.1). Связь между относительными и абсолютными координатами выражается соотношениями:
x=ξ-ξ0, y=η-η0.
После перехода к подвижным координатам уравнения относительного движения частицы примут вид:
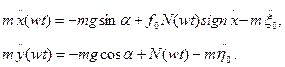 (5п.4)
(5п.4)
Полученная система двух нелинейных уравнений содержит три неизвестные величины: горизонтальное х и вертикальное у смещение частицы относительно лотка и его реакция N(wt). Для исключения неопределенности необходимо привлечь к рассмотрению дополнительные физические соображения о характере движения частицы. С этой целью проанализируем возможные относительные состояния частицы за один период колебаний лотка, а именно: 1) относительный покой, когда частица неподвижна относительно лотка; 2) относительное скольжение, когда частица скользит вдоль лотка без отрыва от его поверхности и 3) полет, когда частица отрывается от лотка (режим движения с подбрасыванием ).
В случае относительного покоя относительные перемещения отсутствуют, т. е. х = у = 0. Тогда из второго уравнения системы (5п.4) следует, что нормальная реакция
 (5п.5)
(5п.5)
При этом из первого уравнения (5п.4) получаем условие относительного покоя:
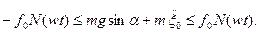 (5п.6)
(5п.6)
Скольжение частицы без отрыва от поверхности определяется
условием:
х≠0, у=0.
При этом нормальная реакция
N(wt) >0 (5п.7)
и определяется выражением (5п.5).
Таким образом, из первого уравнения системы (5п.4) с учетом (5п.5) следует уравнение безотрывного движения частицы:
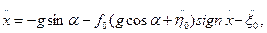 (5п.8)
(5п.8)
причем в соответствии с условием (5п.7) из (5п.5) следует, что
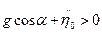 (5п.9)
(5п.9)
Из (5п.9) можно получить условие безотрывного движения частицы:
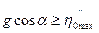 (5п.10)
(5п.10)
где 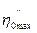 - амплитуда поперечной составляющей вибрации лотка.
- амплитуда поперечной составляющей вибрации лотка.
Отрыв частицы от поверхности лотка и последующий полет характеризуется отсутствием нормальной реакции, т. е.:
N≡0 (5п.11)
Из системы уравнений (5п.4) при условии (5п.11) следуют уравнения, описывающие полет частицы над поверхностью лотка:
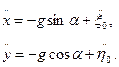 (5п.12)
(5п.12)
Начальные условия для каждого из возможных состояний частицы и режимов ее движения устанавливаются из анализа предшествующего состояния.
Пусть, например, частица лежит неподвижно на лотке. Это состояние описывается соотношениями (5п.5) и (5п.6). При нарушении условия (5п.6) начнется скольжение. Таким образом, определяются начальные условия режима скольжения, описываемого уравнением (5п.8) при соблюдении условия (5п.9). Если на этапе скольжения условие (5п.9) нарушится, то начнется полет, описываемый уравнениями (5п.12), с начальными условиями, соответствующими концу этапа скольжения. Длительность этапа полета τп будет определяться из решения системы (5п.12) при условии, что в конце полета поперечное перемещение частицы у = 0 и реакция N>0. В результате интегрирования (5п.12) вычисляются значения координат и скоростей частицы в конце этапа полета при t= τп, т. е.
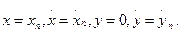 (5п.13)
(5п.13)
Следующий этап (покой, скольжение или вновь полет) будет определяться условиями ударного взаимодействия частицы с лотком.
В задачах рассматриваемого класса обычно предполагают, что соударение происходит практически мгновенно, причем в процессе удара изменение претерпевают относительные скорости частицы, а влиянием удара на движение лотка пренебрегают. Для вычисления относительных скоростей частицы после удара о лоток можно воспользоваться гипотезой Ньютона о пропорциональности относительных скоростей частицы до и после удара:
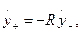 (5п.14)
(5п.14)
где индекс «+» соответствует значению скорости после удара, а индекс «-» соответствует значению скорости до удара; R - коэффициент восстановления нормальной скорости (0≤R≤1). Случай R=0 соответствует абсолютно пластическому удару, когда частица после падения не отскакивает от лотка, случай R=1 соответствует абсолютно упругому удару, когда нормальная составляющая послеударной скорости равна по модулю нормальной составляющей до ударной скорости.
Изменение продольной составляющей скорости частицы при ударе описывается с помощью коэффициента мгновенного трения λ при ударе (0≤λ≤1):
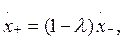
Коэффициенты R и λ устанавливаются экспериментально. В практических расчетах обычно используются граничные значения коэффициентов R и λ.
Соотношения (5п.13) при учете (5п.14) определяют начальные условия последующего этапа движения частицы.
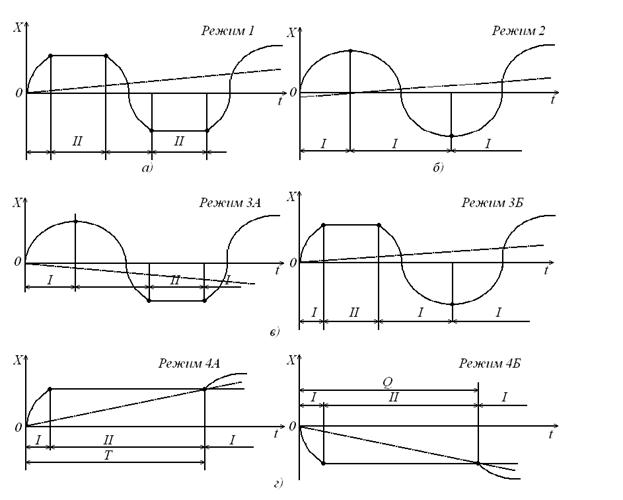
Рис.5.2. Основные режимы движения частицы по вибрирующей плоскости
Изложенный алгоритм позволяет описать основные режимы движения частицы по вибрирующей плоскости. В соответствии с известной классификацией различают следующие режимы безотрывного движения частицы:
· режим 1: скольжение частицы «вперед-назад» с двумя длительными остановками в каждом периоде;
· режим 2: скольжение «вперед-назад» с двумя мгновненными остановками в каждом периоде;
· режим 3: скольжение «вперед-назад» с одной длительной и одной мгновенной остановками в каждом периоде; здесь различают случаи, когда мгновенная остановка следует после скольжения «вперед»(режим 3А) и когда мгновенная остановка следует после скольжения «назад» (режим 3Б);
· скольжение в одном направлении (либо «вперед» - режим 4А, либо «назад» - режим 4Б) с одной длительной остановкой в каждом периоде.
На представленных графиках видно, что за один период колебаний накапливается отличное от нуля смещение частицы «в среднем»; среднее значение функции x(wt) изображено на рис.5.2 штрихпунктирной линией.
 2014-02-12
2014-02-12 1340
1340
