Лекция 7. РЕШЕНИЕ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА С ПОМОЩЬЮ РЯДОВ
Задания для самостоятельной работы
Проинтегрировать уравнения Эйлера.
6.1. 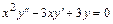 . 6.2.
. 6.2. 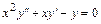 .
.
6.3. 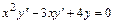 . 6.4.
. 6.4. 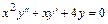 .
.
6.5. 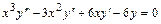 . 6.6.
. 6.6. 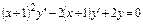 .
.
6.7. 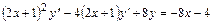 .
.
6.8. 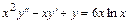 . 6.9.
. 6.9. 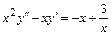 .
.
6.10. 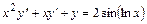 .
.
Привести уравнения к уравнениям с постоянными коэффициентами и найти их решения.
6.11. 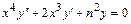 . 6.12.
. 6.12. 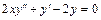 .
.
6.13. 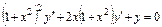 . 6.14.
. 6.14. 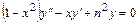 .
.
Пусть дано уравнение
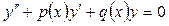 (7.1)
(7.1)
и поставлены начальные условия
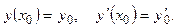 (7.2)
(7.2)
Если коэффициенты уравнения (7.1) р (х) и q (x) разложимы в степенные ряды по степеням 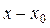 :
:
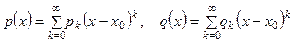 , (7.3)
, (7.3)
сходящиеся в области 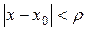 , то уравнение (7.1) имеет единственное решение у = у (х), удовлетворяющее начальным условиям (7.2) и разложимое в сходящийся в той же области
, то уравнение (7.1) имеет единственное решение у = у (х), удовлетворяющее начальным условиям (7.2) и разложимое в сходящийся в той же области 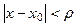 , что и ряды (7.3), степенной ряд разности
, что и ряды (7.3), степенной ряд разности 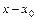 :
:
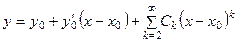 . (7.4)
. (7.4)
Если заданы числа у 0 и 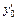 , коэффициенты ряда (7.4) определяются единственным образом, например, подстановкой ряда (7.4) в уравнение (7.1) и приравниванием нулю коэффициентов при различных степенях
, коэффициенты ряда (7.4) определяются единственным образом, например, подстановкой ряда (7.4) в уравнение (7.1) и приравниванием нулю коэффициентов при различных степенях 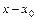 в левой части полученного равенства.
в левой части полученного равенства.
Для построения общего решения уравнения (7.1) достаточно найти два линейно независимых частных решения у 1 и у 2. Обычно строят фундаментальную систему решений у 1 и у 2, нормированную в точке х = х 0, так что: 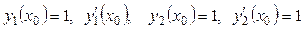 .
.
Если ряд (7.4) представляющий решение уравнения (7.1), удается просуммировать, то есть выразить его сумму через элементарные функции, то второе частное решение можно найти по формуле
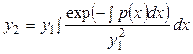 (7.5)
(7.5)
Пример 7.1. Для уравнения
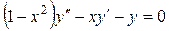
найти фундаментальную систему решений, нормированную в точке х =0 и построить общее решение.
▲ Представим исходное уравнение в виде
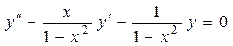 .
.
Коэффициенты этого уравнения 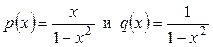 разлагаются в ряды по степеням х, сходящиеся в области
разлагаются в ряды по степеням х, сходящиеся в области 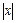 < 1. Поэтому для этого уравнения существуют частные решения у 1 и у 2, представимые в виде степенных рядов (7.4), причем эти ряды, сходятся по крайней мере при
< 1. Поэтому для этого уравнения существуют частные решения у 1 и у 2, представимые в виде степенных рядов (7.4), причем эти ряды, сходятся по крайней мере при 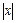 <1.
<1.
Найдем у 1 нормированное в точке х =0, для представим его в виде ряда
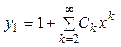
и вычислим 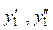 :
:
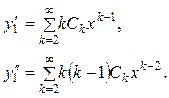
Подставив найденные выражения 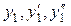 в исходное уравнение, получим:
в исходное уравнение, получим:
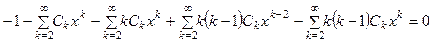 .
.
Далее приравняв коэффициенты при одинаковых степенях х, найдем значения всех коэффициентов:
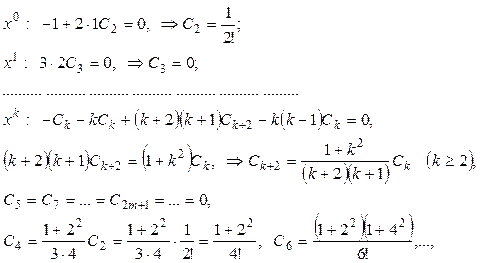
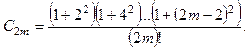
Таким образом,
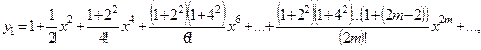
Частное решение у 2 ищем в виде
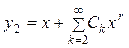
После подстановки этого решения и его производных в исходное уравнение мы, так же, как и проделывали выше, найдем все коэффициенты Ck. В результате получим
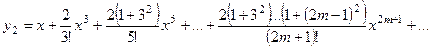
Таким образом, общим решением исходного уравнения будет:
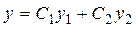 .▲
.▲
 2014-02-12
2014-02-12 613
613








