Многие задачи математики и физики приводят к дифференциальным уравнениям 2-го порядка вида (7.1), коэффициенты которых – рациональные функции
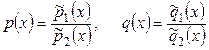 (7.6)
(7.6)
где 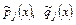 - многочлены. Можно считать, что эти дроби несократимы; тогда в точках, в которых
- многочлены. Можно считать, что эти дроби несократимы; тогда в точках, в которых 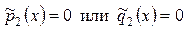 , хотя бы один из коэффициентов уравнения (7.1) обратится в бесконечность. Такие точки будут особыми точками уравнения (7.1).
, хотя бы один из коэффициентов уравнения (7.1) обратится в бесконечность. Такие точки будут особыми точками уравнения (7.1).
Пусть х = х 0 – особая точка уравнения (7.1), тогда в окрестности этой точки решение уравнения (100) невозможно представить в виде простого степенного ряда (103). Однако, в этом случае решение можно представить в виде сходящегося в области 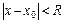 обобщенного степенного ряда вида:
обобщенного степенного ряда вида:
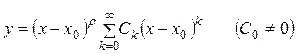 . (7.7)
. (7.7)
Для определения показателя r и коэффициентов Сk нужно подставить ряд (7.7) в уравнение (7.1), сократить на 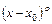 и приравнять нулю коэффициенты при различных степенях х – х 0. При этом число r находится из так называемого определяющего уравнения в особой точке х = х 0:
и приравнять нулю коэффициенты при различных степенях х – х 0. При этом число r находится из так называемого определяющего уравнения в особой точке х = х 0:
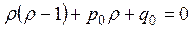 . (7.8)
. (7.8)
Коэффициенты p 0 и q 0 этого уравнения можно найти по формулам:
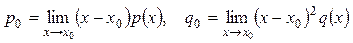 . (7.9)
. (7.9)
В случае, когда корни 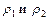 определяющего уравнения (7.8) различны, уравнение (7.1) всегда имеет решение вида (7.7), где r есть тот из корней
определяющего уравнения (7.8) различны, уравнение (7.1) всегда имеет решение вида (7.7), где r есть тот из корней 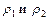 , который имеет большую вещественную часть. Если
, который имеет большую вещественную часть. Если 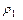 - этот корень, то решение имеет вид
- этот корень, то решение имеет вид
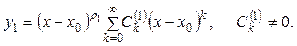 (7.10)
(7.10)
Если разность корней 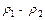 определяющего уравнения (7.8) не является целым положительным числом, то существует решение в виде обобщенного степенного ряда, соответствующее и второму корню
определяющего уравнения (7.8) не является целым положительным числом, то существует решение в виде обобщенного степенного ряда, соответствующее и второму корню 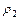 :
:
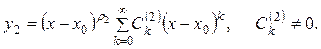 (7.11)
(7.11)
Если же 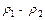 есть целое положительное число, то второе частное решение или снова имеет вид (7.11), или же представляет собой сумму обобщенного степенного ряда и произведения некоторого обобщенного степенного ряда на ln (x – x 0):
есть целое положительное число, то второе частное решение или снова имеет вид (7.11), или же представляет собой сумму обобщенного степенного ряда и произведения некоторого обобщенного степенного ряда на ln (x – x 0):
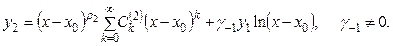 (7.12)
(7.12)
Наконец, если корни определяющего уравнения (7.8) равны между собой 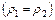 , тот существует только одно частное решение в виде обобщенного степенного ряда. Второе же решение обязательно содержит ln(x – x 0). Его следует искать в виде
, тот существует только одно частное решение в виде обобщенного степенного ряда. Второе же решение обязательно содержит ln(x – x 0). Его следует искать в виде
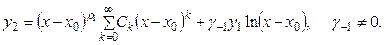 (7.13)
(7.13)
При решении многих прикладных задач, в частности при решении задач о распространении тепла в различных объектах приходя к линейному дифференциальному уравнению вида
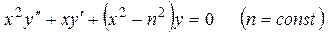 (7.14)
(7.14)
Это уравнение называется уравнением Бесселя. Так как это уравнение имеет особую точку х =0, то его частное решение будем искать в виде обобщенного степенного ряда:
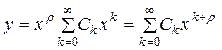 (С 0 ≠ 0) (7.15)
(С 0 ≠ 0) (7.15)
Дифференцируя этот ряд дважды
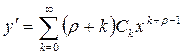 , (7.16)
, (7.16)
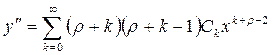 , (7.17)
, (7.17)
и подставляя выражения (7.15), (7.16) и (7.17) в исходное уравнение (7.14), получим
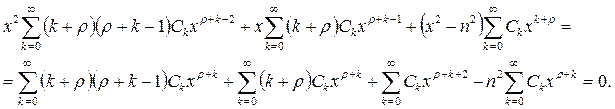
В полученном уравнении выделим члены при k = 0 и k = 1
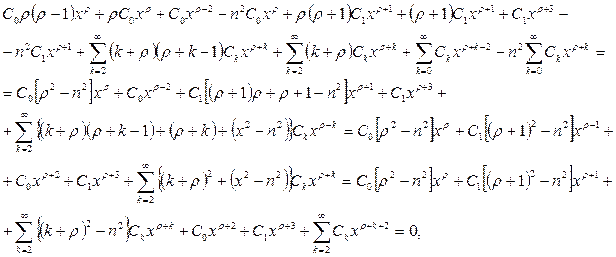
так как
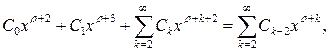
то окончательно уравнение принимает вид
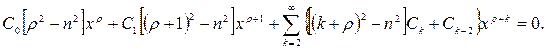 (7.18)
(7.18)
Сравнивая коэффициенты при одинаковых степенях х в левой и правой частях того уравнения, получим систему
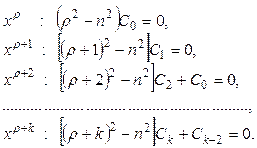
Так как коэффициент при С 0 при низшей степени х можно считать отличным от нуля, то первое уравнение сводится к
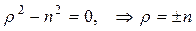 .
.
Будем считать, что 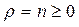 ; тогда из второго уравнения
; тогда из второго уравнения
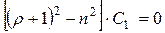 ,
,
получим 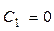 , так как
, так как 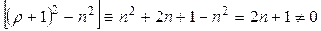 , при любом значении п.
, при любом значении п.
Рассмотрим последнее уравнение системы
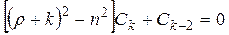 ,
,
и придавая k значения 3,5,7,…, заключаем, что
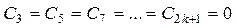 . (7.19)
. (7.19)
Для коэффициентов с четными номерами получаем выражения
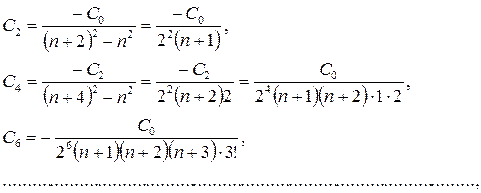
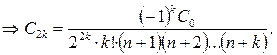 (7.20)
(7.20)
По условию задачи С 0 ≠ 0, и поэтому Бессель предложил коэффициент С 0 выбрать следующим образом
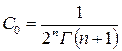 (7.21)
(7.21)
где 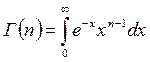 - гамма-функция Эйлера, обладающая рядом свойств, например:
- гамма-функция Эйлера, обладающая рядом свойств, например:
1. 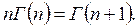 (7.22)
(7.22)
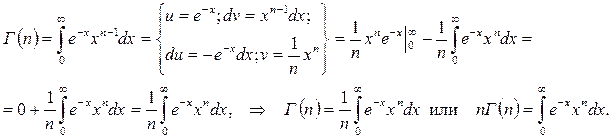
С другой стороны
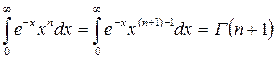
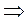
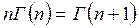 .
.
2. 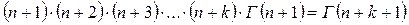 . (7.23)
. (7.23)
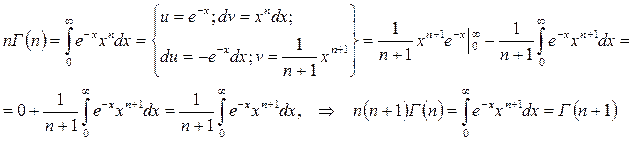
или
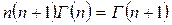 .
.
Продолжаем далее
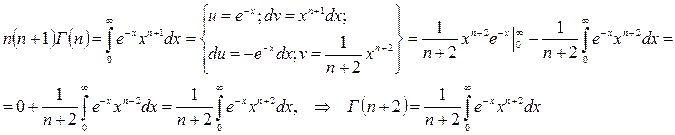 или
или
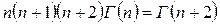 .
.
Продолжая далее, мы придем
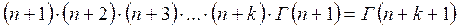 .
.
3. 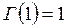 . (7.24)
. (7.24)
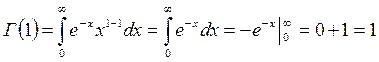 .
.
4. при n = 0 из (7.23) следует, что
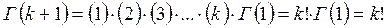 . (7.25)
. (7.25)
Таким образом, с учетом (7.22), (7.23), (7.24) и (7.25) четные коэффициенты будут определяться по формуле
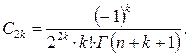 (7.26)
(7.26)
Подставив (7.26) в (7.15), получим для случая, когда 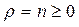 первое частное решение исходного уравнения Бесселя (7.14):
первое частное решение исходного уравнения Бесселя (7.14):
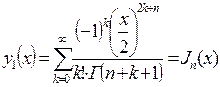 , (7.27)
, (7.27)
где 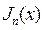 - функция Бесселяпервого рода n-го порядка (или цилиндрической функцией).
- функция Бесселяпервого рода n-го порядка (или цилиндрической функцией).
Найдем второе частное решение уравнения Бесселя (7.14) при 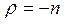 . В этом случае все коэффициенты Сk совершенно аналогично определяются только в случае, когда п не равно целому числу. Тогда решение можно получить, заменяя в предыдущем решении величину п на – п:
. В этом случае все коэффициенты Сk совершенно аналогично определяются только в случае, когда п не равно целому числу. Тогда решение можно получить, заменяя в предыдущем решении величину п на – п:
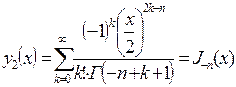 . (7.28)
. (7.28)
Пусть n – целое положительное число, тогда при k = 0,1,2,…, n -1 величина – n + k +1 принимает отрицательные значения и 0
n =1; k =0 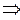 -1+0+1=0;
-1+0+1=0;
n =2; k =0 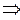 -2+0+1=-1;
-2+0+1=-1;
k =1 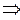 -2+1+1=0;
-2+1+1=0;
n =3; k =0 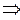 -3+0+1=-2;
-3+0+1=-2;
k =1 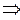 -3+1+1=-1;
-3+1+1=-1;
k =2 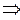 -3+2+1=0;
-3+2+1=0;
и т.д.
Для этих значений 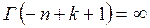 , т.к.
, т.к. 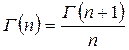 , следовательно первые n членов в (7.28) в 0, и
, следовательно первые n членов в (7.28) в 0, и
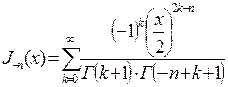 .
.
Пусть k = n + l, тогда
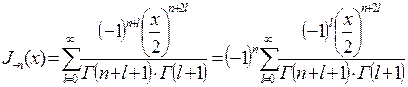 ,
,
С учетом того, что
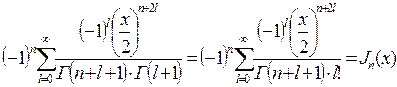 ,
,
Получается
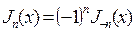 , (7.29)
, (7.29)
А это равенство свидетельствует о том, что функции 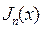 и
и 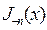 являются линейно зависимыми, поэтому решение (7.28) не может быть вторым частным решением исходного уравнения Бесселя (7.14).
являются линейно зависимыми, поэтому решение (7.28) не может быть вторым частным решением исходного уравнения Бесселя (7.14).
Для нахождения второго, линейно-независимого от 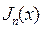 решения введем новую функцию Yn (x), представив ее в виде
решения введем новую функцию Yn (x), представив ее в виде
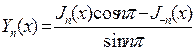 . (7.30)
. (7.30)
Очевидно, что эта функция также будет являться решением (7.14), так как она представляет собой линейную комбинацию частных решений 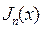 и
и 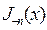 этого уравнения. Нетрудно убедиться на основании равенства (7.29), что при n, равном целому числу, правая часть равенства (7.30) принимает неопределенный вид
этого уравнения. Нетрудно убедиться на основании равенства (7.29), что при n, равном целому числу, правая часть равенства (7.30) принимает неопределенный вид  .Раскрывая эту неопределенность по правилу Лопиталя, получим следующее представление функции Yn (x) при целом положительном n:
.Раскрывая эту неопределенность по правилу Лопиталя, получим следующее представление функции Yn (x) при целом положительном n:
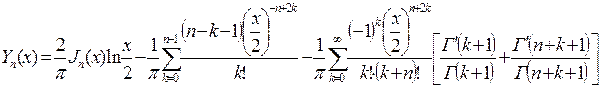 (7.31)
(7.31)
В частном случае, при n = 0, функция Yn (x) представляется таким образом:
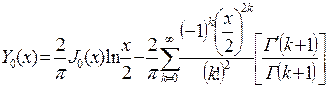 (7.32)
(7.32)
Функция Yn (x) называется функцией Бесселя 2-го рода n-го порядка или функцией Вебера.
Функции Jn (x) и Yn (x) являются линейно-независимыми, следовательно, эти функции при всяком n образуют фундаментальную систему решений и поэтому общее решение уравнения Бесселя (7.14) имеет вид:
y = C 1 Jn (x) + C 2 Yn (x). (7.33)
где С 1 и С 2 – произвольные постоянные.
Пример 7.2. Найти функцию Бесселя при п = 0.
▲ Воспользовавшись равенством
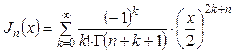 .
.
При п = 0 получим
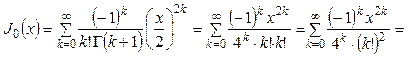
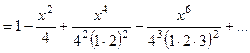 ▲
▲
Пример 7.3. Решить уравнение
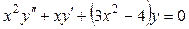 .
.
▲ Это уравнение Бесселя, которое может быть записано в виде:
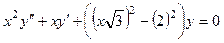 .
.
Следовательно, общее решение уравнения имеет вид:
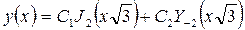 .▲
.▲
Пример 7.4. Решить уравнение
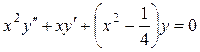 .
.
▲ Так как в этом уравнении п = ½, то общее решение уравнения имеет вид
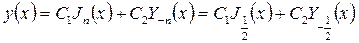 ,
,
где -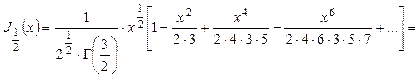
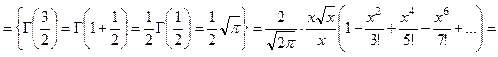
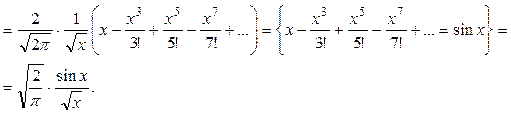
Точно так же получим и 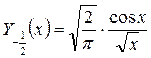 . Следовательно, общее решение исходного уравнения будет иметь вид:
. Следовательно, общее решение исходного уравнения будет иметь вид:
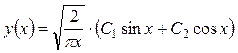 .▲
.▲
 2014-02-12
2014-02-12 1703
1703
