Лекция 6. ЛИНЕЙНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ С ПЕРЕМЕННЫМИ КОЭФФИЦИЕНТАМИ
Линейным уравнением п -го порядка с переменными коэффициентами называется уравнение вида
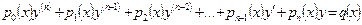 , (6.1)
, (6.1)
где все 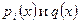 непрерывные на некотором отрезке [a,b] функции. Считая
непрерывные на некотором отрезке [a,b] функции. Считая 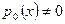 можно разделив уравнение (26) на
можно разделив уравнение (26) на 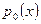 и вводя новые обозначения
и вводя новые обозначения
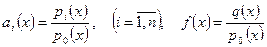 ,
,
представить уравнение (26) в виде:
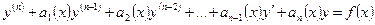 . (6.2)
. (6.2)
Если при всех значениях х функция f(x) равна нулю, то уравнение (6.2) будет называться однородным линейным уравнением
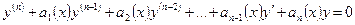 , (6.3)
, (6.3)
в противном случае – неоднородным линейным уравнением.
Левая часть уравнения (6.3) может обозначаться кратко через линейный дифференциальный оператор -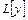 . Тогда уравнение (6.3) можно записать в виде
. Тогда уравнение (6.3) можно записать в виде
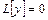 (6.3* )
(6.3* )
Поскольку коэффициенты 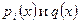 уравнения (6.1) являются непрерывными на отрезке [a,b] функциями, то и коэффициенты
уравнения (6.1) являются непрерывными на отрезке [a,b] функциями, то и коэффициенты 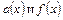 уравнения (6.2) также будут непрерывными на отрезке [a,b] функциями. Тогда уравнения (6.1) и (6.2) будут иметь единственное решение у = у (х), определенное во всем интервале [a,b] и удовлетворяющее начальным условиям:
уравнения (6.2) также будут непрерывными на отрезке [a,b] функциями. Тогда уравнения (6.1) и (6.2) будут иметь единственное решение у = у (х), определенное во всем интервале [a,b] и удовлетворяющее начальным условиям:
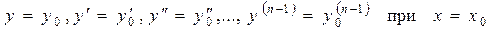 , (6.4)
, (6.4)
причем начальные данные 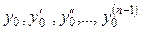 можно задавать совершенно произвольно, а х 0 нужно брать из интервала [a,b].
можно задавать совершенно произвольно, а х 0 нужно брать из интервала [a,b].
Вронскиан п решений однородного линейного уравнения п -го порядка связан с первым коэффициентом уравнения (6.3) 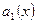 формулой Остроградского – Лиувилля:
формулой Остроградского – Лиувилля:
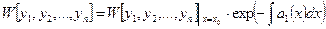 . (6.5)
. (6.5)
Формула Остроградского-Лиувилля может быть использована для интегрирования линейного уравнения второго порядка вида
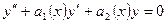 , (6.6)
, (6.6)
если известно одно нетривиальное решение этого уравнения 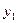 . Согласно формуле Остроградского-Лиувилля любое решение этого уравнения второго порядка должно быть также решением уравнения
. Согласно формуле Остроградского-Лиувилля любое решение этого уравнения второго порядка должно быть также решением уравнения
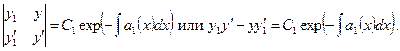
Для интегрирования этого линейного уравнения первого порядка можно воспользоваться методом интегрирующего множителя. Умножая на 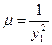 , получи
, получи
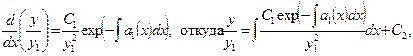
или
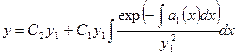 . (6.7)
. (6.7)
Пример 6.1. Найти общее решение уравнения: 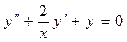 , если известно одно его частное решение
, если известно одно его частное решение 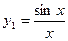 .
.
▲ По формуле (6.7) находим
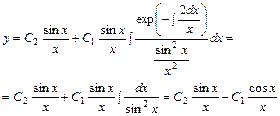 .▲
.▲
 2014-02-12
2014-02-12 1131
1131
