Линейные уравнения с переменными коэффициентами вида
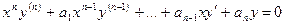 (6.8)
(6.8)
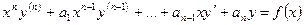 (6.9)
(6.9)
или
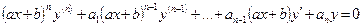 (6.10)
(6.10)
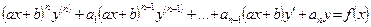 (6.11)
(6.11)
называются уравнением Эйлера. Здесь 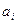 - постоянные коэффициенты.
- постоянные коэффициенты.
С помощью подстановки
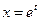 (6.12)
(6.12)
для уравнения (6.8), (6.9) и
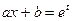 (6.13)
(6.13)
для уравнения (6.10), (6.11) оба эти уравнения сводятся к уравнению с постоянными коэффициентами. Для этого необходимо вычислить производные, например, от (6.12) по новой переменной t:
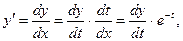
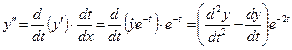 , (6.14)
, (6.14)
……………………………………………………………
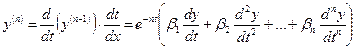 .
.
Подставив значения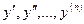 (6.14) в уравнение (6.8), получим новое уравнение с постоянными коэффициентами
(6.14) в уравнение (6.8), получим новое уравнение с постоянными коэффициентами 
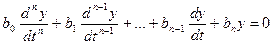 , (6.15)
, (6.15)
которое называется преобразованным уравнением, по отношению к уравнению (6.8). Интегрируя это уравнение, находится решение 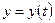 и далее после возвращения к старой переменной в соответствии с формулой (6.12) -
и далее после возвращения к старой переменной в соответствии с формулой (6.12) - 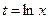 , найдем решение уравнения (6.8). Решения уравнений (6.9), (6.10), (6.11) находятся аналогичным способом.
, найдем решение уравнения (6.8). Решения уравнений (6.9), (6.10), (6.11) находятся аналогичным способом.
Пример 6.2. Найти решение уравнения: 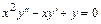 .
.
▲ Полагая 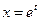 или
или 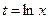 , найдем
, найдем 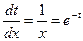 .
.
Вычислим производные по новой переменной t, обозначив точками дифференцирование по t:
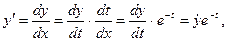
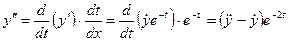 .
.
Подставив 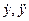 в исходное уравнение, получим
в исходное уравнение, получим
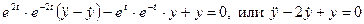 .
.
Следовательно, мы получили однородное линейное уравнение. Его характеристическое уравнение 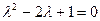 имеет корни
имеет корни 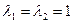 . Поскольку корни действительные и кратные, с кратностью равной двум, то общее решение будет иметь вид:
. Поскольку корни действительные и кратные, с кратностью равной двум, то общее решение будет иметь вид:
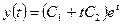 .
.
Перейдя к переменной х, окончательно получим общее решение исходного уравнения
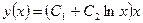 .▲
.▲
Пример 6.3. Найти решение уравнения:
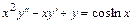 .
.
▲ Полагая 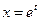 или
или 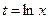 , найдем
, найдем 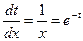 .
.
Вычислим производные по новой переменной t, обозначив точками дифференцирование по t:
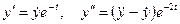 .
.
Подставив 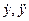 в исходное уравнение, получим
в исходное уравнение, получим
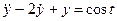 . (П6.3.1)
. (П6.3.1)
Это неоднородное линейное уравнение с постоянными коэффициентами и общее решение соответствующего ему однородного уравнения 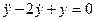 имеет вид
имеет вид
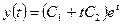 ,
,
Поскольку характеристическое уравнение 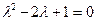 имеет двукратный корень равный единице:
имеет двукратный корень равный единице: 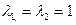 .
.
Частное решение уравнения (П6.3.1)можно получить методом неопределенных коэффициентов.
Поскольку параметры правой части неоднородного уравнения (П6.3.1) равны, соответственно, a =0, b = 1, q = 0, l = 0 и число 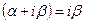 не совпадает ни с одним корнем характеристического уравнения, поэтому s =0, и m = max(q,l) = 0. Исходя из этого, можно выписать вид искомого частного решения:
не совпадает ни с одним корнем характеристического уравнения, поэтому s =0, и m = max(q,l) = 0. Исходя из этого, можно выписать вид искомого частного решения:
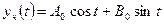
Вычислим производные от 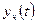
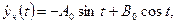
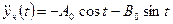
и подставив их в уравнение (П6.3.1), получим
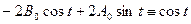 .
.
Приравняем коэффициенты при одинаковых функциях в правой и левой частях этого уравнения
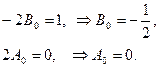
Следовательно, частное решение уравнения (П6.3.1) имеет вид
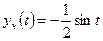 ,
,
а общее решение уравнения (П6.3.1) будет выглядеть так:
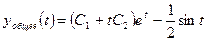 .
.
Таким образом, общее решение исходного уравнения имеет вид:
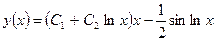 .▲
.▲
Частные решения однородного уравнения Эйлера (6.8), также можно получить, если использовать подстановку вида:
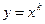 (6.16)
(6.16)
Вычислив производные
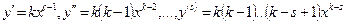 ,
,
и подставив их в уравнение (6.8) и сокращая на 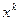 , получим
, получим
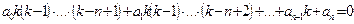 (6.17)
(6.17)
Это уравнение п -ой степени относительно k имеет п корней: 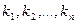 ; если все корни различны, то мы получаем п линейно независимых частных решений
; если все корни различны, то мы получаем п линейно независимых частных решений 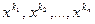 , следовательно, общее решение будет иметь вид:
, следовательно, общее решение будет иметь вид:
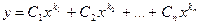 . (6.18)
. (6.18)
Пример 6.4. Найти решение уравнения:
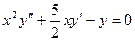 .
.
▲ Ищем решение в виде 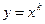 , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
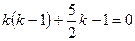 ,
,
откуда 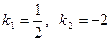 . Мы видим, что корни действительные и различные, поэтому общее решение при х > 0 имеет вид
. Мы видим, что корни действительные и различные, поэтому общее решение при х > 0 имеет вид
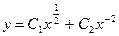 .▲
.▲
Кроме того, уравнение (6.17) будет характеристическим уравнением для преобразованного уравнения (6.15)
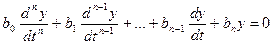 ,
,
так как 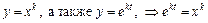 . Следовательно, кратному корню
. Следовательно, кратному корню 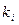 кратности a уравнения (6.17) будут соответствовать частные решения преобразованного уравнения
кратности a уравнения (6.17) будут соответствовать частные решения преобразованного уравнения
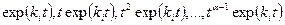
а общее решение преобразованного уравнения будет иметь вид:
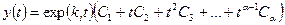 .
.
С учетом того, что 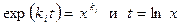 , общее решение уравнения Эйлера принимает вид:
, общее решение уравнения Эйлера принимает вид:
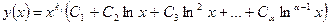 .
.
Пример 6.5. Найти решение уравнения: 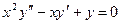 .
.
▲ Ищем решение в виде 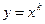 , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
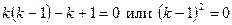 ,
,
откуда 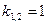 Мы видим, что корни кратные с кратностью равной 2, поэтому общее решение при х > 0 имеет вид:
Мы видим, что корни кратные с кратностью равной 2, поэтому общее решение при х > 0 имеет вид: 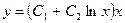 .▲
.▲
Комплексным сопряженным корням 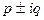 кратности a уравнения (6.17) будут соответствовать частные решения
кратности a уравнения (6.17) будут соответствовать частные решения
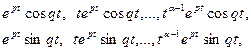
преобразованного уравнения или с учетом того, что 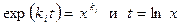 частные решения
частные решения
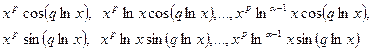
исходного уравнения Эйлера.
Пример 6.6. Найти решение уравнения: 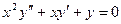 .
.
▲ Ищем решение в виде 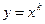 , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
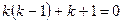 ,
,
откуда 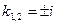 , Мы видим, что корни комплексные, поэтому общее решение при х > 0 имеет вид
, Мы видим, что корни комплексные, поэтому общее решение при х > 0 имеет вид
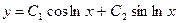 .▲
.▲
Пример 6.7. Найти решение уравнения:
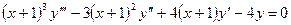 .
.
▲ Это уравнение Эйлера вида (6.10), поэтому его решение ищем в виде 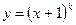 , тогда уравнение (6.17) принимает вид:
, тогда уравнение (6.17) принимает вид:
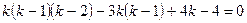 ,
,
откуда 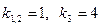 , Мы видим, что корни действительные и различные, причем среди них имеется двукратный корень-
, Мы видим, что корни действительные и различные, причем среди них имеется двукратный корень-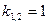 . Поэтому частными решениями будут
. Поэтому частными решениями будут
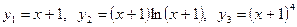 ,
,
а общее решение имеет вид
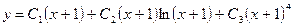 .▲
.▲
 2014-02-12
2014-02-12 1826
1826
