Задачи для самостоятельной работы
Найти решения уравнений в виде степенных или обобщенно степенных рядов.
7.1. 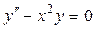 . 7.2.
. 7.2. 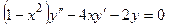 . 7.3.
. 7.3. 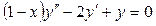 .
.
7.4. 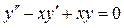 . 7.5.
. 7.5. 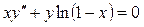 . 7.6.
. 7.6. 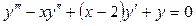 .
.
7.7. 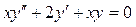 . 7.8.
. 7.8. 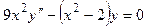 . 7.9.
. 7.9. 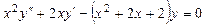 .
.
Нормальная система обыкновенных дифференциальных уравнений имеет вид:
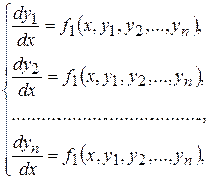 (8.1)
(8.1)
или
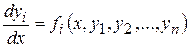 , (8.2)
, (8.2)
где 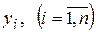 - неизвестные функции от независимой переменной х, подлежащие определению, а
- неизвестные функции от независимой переменной х, подлежащие определению, а 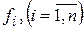 - известные функции от
- известные функции от 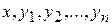 , заданные и непрерывные в некоторой области. Число n называется порядком системы (8.1) и (8.2).
, заданные и непрерывные в некоторой области. Число n называется порядком системы (8.1) и (8.2).
Если правые части системы уравнений (8.1) или (8.2) являются линейными функциями от 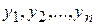 , то такая система будет называться линейной.
, то такая система будет называться линейной.
Совокупность п функций
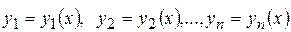 , (8.3)
, (8.3)
определенных и непрерывно дифференцируемых в интервале (a,b), называется решением системы (8.1) или (8.2) в этом интервале (a,b), если функции (8.3), обращают уравнение (8.1) или (8.2) в тождества, справедливые при всех значениях х из интервала (a,b).
Кривая в (n +1)-мерном пространстве (x, y 1, y 2,…, yn), соответствующая решению (8.3), называется интегральной кривой.
Задача нахождения решения (8.3), удовлетворяющего начальным условиям:
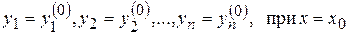 , (8.4)
, (8.4)
где 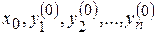 - заданные числа (начальные данные), называется задачей Коши (начальной задачей).
- заданные числа (начальные данные), называется задачей Коши (начальной задачей).
Для существования и единственности решения задачи Коши необходимо и достаточно, чтобы правые части системы (8.1) или (8.2) были не только непрерывными в окрестности точки (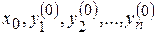 ), но и имели бы в этой точке ограниченные частные производные по
), но и имели бы в этой точке ограниченные частные производные по 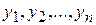 , то есть правые части системы (8.1) или (8.2) удовлетворяли бы условию Липшица относительно
, то есть правые части системы (8.1) или (8.2) удовлетворяли бы условию Липшица относительно 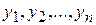 в окрестности точки (
в окрестности точки (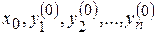 ).
).
Совокупность п функций
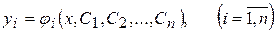 , (8.5)
, (8.5)
определенных в некоторой области изменения переменных 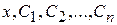 и имеющих частные производные по х, будет называться общим решением системы (1) или (2) в области D изменения переменных
и имеющих частные производные по х, будет называться общим решением системы (1) или (2) в области D изменения переменных 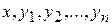 , в каждой точке которой имеет место существование и единственность решения задачи Коши, если:
, в каждой точке которой имеет место существование и единственность решения задачи Коши, если:
1. система уравнений (8.5) разрешима в области D относительно произвольных постоянных 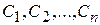 , а именно:
, а именно:
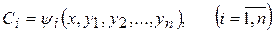 . (8.6)
. (8.6)
2. совокупность функций (8.5) является решением системы (8.1) или (8.2) при всех значениях произвольных постоянных, доставляемых уравнениями (8.6), когда точка (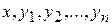 ) пробегает область D.
) пробегает область D.
Решение (8.3), в каждой точке которой имеет место существование и единственность решения задачи Коши, называется частным решением. Если в каждой точке решения нарушается единственность решения задачи Коши, то оно называется особым.
Функция 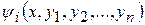 , которую будем предполагать непрерывно дифференцируемой и не сводящейся к постоянной, будет называться интегралом системы (8.1) или (8.2), если она тождественно обращается в постоянную вдоль любого частного решения. Отсюда следует, что
, которую будем предполагать непрерывно дифференцируемой и не сводящейся к постоянной, будет называться интегралом системы (8.1) или (8.2), если она тождественно обращается в постоянную вдоль любого частного решения. Отсюда следует, что 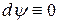 в силу системы (8.1) или (8.2), то есть
в силу системы (8.1) или (8.2), то есть
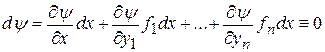
Нормальная система из п уравнений не может иметь более, чем п независимых интегралов.
Равенство 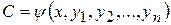 называется первым интегралом системы (8.1) или (8.2). Совокупность всех первых интегралов образует общий интеграл системы (8.1) или (8.2).
называется первым интегралом системы (8.1) или (8.2). Совокупность всех первых интегралов образует общий интеграл системы (8.1) или (8.2).
Всякую нормальную систему (8.1) или (8.2) можно записать в виде:
 , (8.7)
, (8.7)
который называется симметрической формой нормальной системы дифференциальных уравнений.
Нормальная система вида
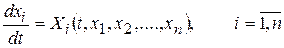 , (8.8)
, (8.8)
где t – время; x 1, x 2,…., xn – координаты точки n – мерного пространства, называется динамической системой, а само n – мерное пространство будет называться фазовым пространством. В случае, когда n = 2 фазовым пространством будет являться плоскость (x 1, x 2), которую называют фазовой плоскостью.
Если правые части систем (8.1) и (8.2) не зависят от переменной х
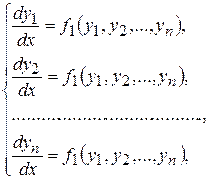 (8.9)
(8.9)
и
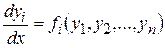 , (8.10)
, (8.10)
а правая часть системы (8.8) от t
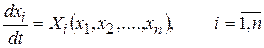 , (8.11)
, (8.11)
то системы (8.9) и (8.10) будут называться стационарными или автономными, а система (8.11) – автономно-динамической системой (АДС).
Всякое решение
x 1= x 1(t), x 2= x 2(t), …., xn = xn (t) (8.12)
динамической системы (8.8) или АДС (8.11) называется движением, определяемым этими системами, а путь, описываемый движущейся точкой в фазовом пространстве, траекторией этого движения.
Рассмотрим методы решения систем.
1. Метод исключения. Суть данного метода заключается в том, что путем последовательного дифференцирования одного из уравнений системы и исключением всех неизвестных функций, кроме одной, получают одно уравнение относительно этой функции. Поэтому метод исключения также называют методом сведения системы уравнений к одному уравнению более высокого порядка.
Пример 8.1. Решить систему:
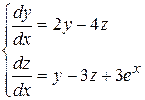
▲ Для нахождения решения этой системы методом исключения необходимо продифференцировать одно из уравнений системы и произвести такие преобразования, в результате которых получим одно уравнение относительно одной функции. Например, продифференцировав первое уравнение системы, получим
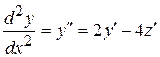 .
.
Подставив в это уравнение значение производной функции z из второго уравнения исходной системы, получим
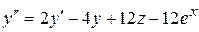 .
.
Далее, выразив из первого уравнения исходной системы функцию z и, подставив ее в последнее уравнение, окончательно получим уравнение
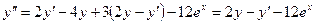
или
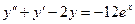 (П8.1)
(П8.1)
которое является неоднородным линейным уравнением второго порядка. Для того, чтобы найти общее решение этого уравнения, необходимо найти общее решение соответствующего ему однородного уравнения 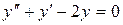 , а затем найти частное решение исходного неоднородного уравнения. Для этого можно использовать, например, метод неопределенных коэффициентов.
, а затем найти частное решение исходного неоднородного уравнения. Для этого можно использовать, например, метод неопределенных коэффициентов.
Для нахождения общего решения однородного уравнения составим соответствующее ему характеристическое уравнение
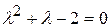 .
.
Корни этого уравнения равны: 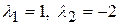 , и являются действительными и различными. Поэтому общее решение однородного уравнения имеет вид:
, и являются действительными и различными. Поэтому общее решение однородного уравнения имеет вид:
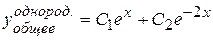 .
.
Теперь найдем частное решение неоднородного уравнения. Правая часть неоднородного уравнения имеет вид: -12 ех, поэтому, по методу неопределенных коэффициентов частное решение будем искать в виде:
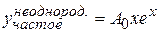 .
.
Найдя первую и вторую производные этого решения, и, подставив их в неоднородное уравнение, получим
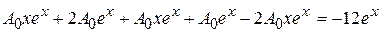
или после сокращений
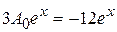 .
.
Из этого равенства можно определить неопределенный коэффициент А 0, приравняв коэффициенты при функции ех
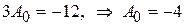 .
.
Таким образом, частное решение неоднородного уравнения (П8.1) имеет вид:
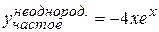 ,
,
а его общее решение, являющееся одновременно одной из искомых функций исходной системы, будет равно
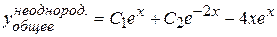 .
.
Вторую искомую функцию z найдем из первого уравнения исходной системы
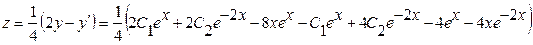
или
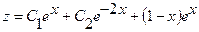
Таким образом, общее решение исходной системы принимает вид:
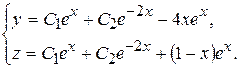 ▲
▲
Пример 8. 2. Для системы
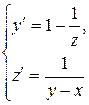
Найти общее решение, удовлетворяющее начальным условиям:
у = -1, z =1 при х = 0.
▲ Для нахождения общего решения данной системы поступим следующим образом: продифференцируем второе уравнение исходной системы
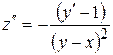 .
.
Далее заменим в этом уравнении 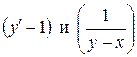 их значениями из исходной системы, а именно
их значениями из исходной системы, а именно 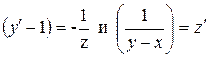 , в результате получим уравнение:
, в результате получим уравнение:
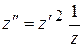 .
.
Это уравнение можно привести к виду
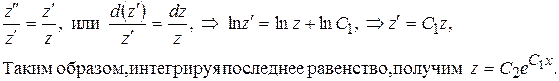
Для нахождения второй искомой функции у необходимо воспользоваться вторым уравнением исходной системы и полученным значением функции z:
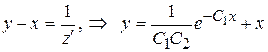 .
.
Таким образом, общим решением исходной системы будет
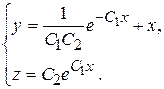
Далее необходимо решит задачу Коши. Для этого подставим начальные условия в полученное решение и найдем значения С 1 =-1и С 2 =1. Следовательно, искомым решением задачи Коши будет решение, имеющее вид:
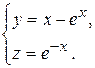 ▲
▲
2. Метод интегрируемых комбинаций. Интегрирование нормальной системы (8.1)
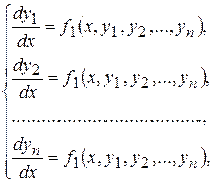
или системы (8.8)
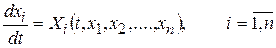 ,
,
облегчается, если удается найти один или несколько независимых первых интегралов исходной системы
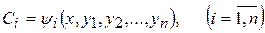 ,
,
т.к. в этом случае удается понизить порядок системы и соответственно уменьшить число искомых функций.
Первые интегралы во многих случаях получаются путем составления так называемых интегрируемых комбинаций.
Интегрируемой комбинацией для исходной системы называется такое дифференциальное уравнение, которое является следствием из исходной системы и которое достаточно легко интегрируется. Количество первых интегралов исходной системы равно количеству, входящих в нее уравнений.
Пример 8.3. Решить систему:
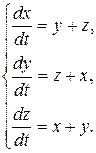
▲ Для нахождения первых независимых интегралов данной системы, сложим эти уравнения почленно, в результате получим:
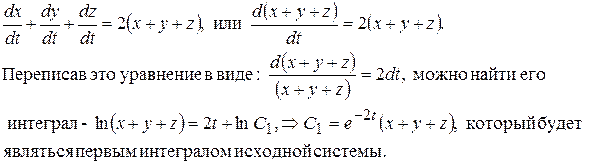
Для нахождения второго интеграла вычтем из первого уравнения системы второе уравнение
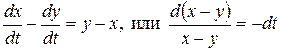 ,
,
следовательно, второй интеграл системы будет равен:
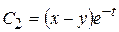 .
.
Для нахождения третьего интеграла вычтем почленно из второго уравнения системы третье:
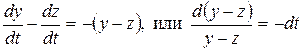 ,
,
следовательно, второй интеграл системы будет равен:
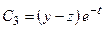 .
.
Таким образом, общий интеграл исходной системы имеет вид:
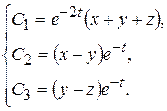 ▲
▲
Пример 8.4. Найти общее решение системы:
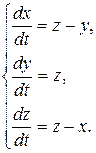
▲Вычтем почленно из первого уравнения исходной системы второе
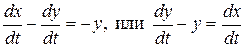 .
.
Далее продифференцируем второе уравнение исходной системы
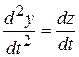
и подставим это выражение вместо 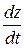 , а функцию z выразим из второго уравнения исходной системы, и также подставим в третье уравнение, в результате получим уравнение
, а функцию z выразим из второго уравнения исходной системы, и также подставим в третье уравнение, в результате получим уравнение
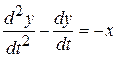 .
.
Далее, продифференцировав еще раз уравнение 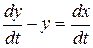 , получим:
, получим: 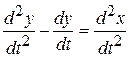 . Сравнив это уравнение с ранее полученным
. Сравнив это уравнение с ранее полученным 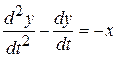 , приходим к уравнению относительно функции х:
, приходим к уравнению относительно функции х:
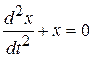 .
.
Данное уравнение является однородным линейным уравнением второго порядка, потому мы можем записать для него характеристическое уравнение 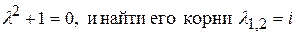 , которые являются исключительно мнимыми, следовательно, общее решение однородного уравнения можно записать в виде:
, которые являются исключительно мнимыми, следовательно, общее решение однородного уравнения можно записать в виде:
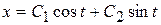 .
.
Продифференцируем полученное выражение и подставим его в уравнение 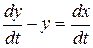 . В результате получим неоднородное линейное уравнение первого порядка относительно второй искомой функции у:
. В результате получим неоднородное линейное уравнение первого порядка относительно второй искомой функции у:
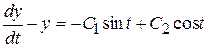 .
.
Для решения этого уравнения используем формулу Эйлера [1-14]:
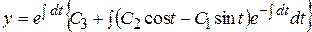 .
.
После интегрирования окончательно получим
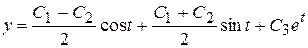 .
.
Третью искомую функцию z можно найти, продифференцировав функцию у:
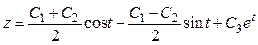 .
.
Таким образом, общее решение исходной системы имеет вид:
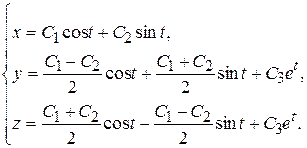 ▲
▲
Пример 8.5. Найти решение системы
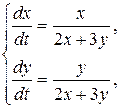
удовлетворяющее начальным условиям: х = 1, у =2 при t = 0.
▲ Составим первую интегрируемую комбинацию, разделив для этого первое уравнение системы на второе
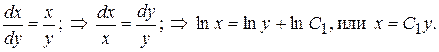
Далее составим вторую интегрируемую комбинацию. Для этого умножим обе части первого уравнения исходной системы на два, а второе уравнение на три, после чего сложим полученные результаты, в итоге получим:
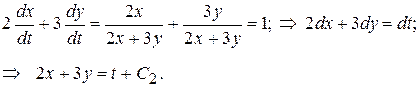
Из системы уравнений
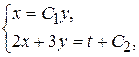
найдем общее решение исходной системы
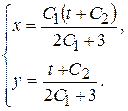
Используя начальные условия, найдем решение задачи Коши:
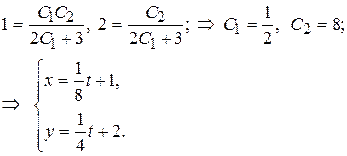 ▲
▲
Пример 8.6. Найти независимые интегралы системы, представленной в симметрической форме:
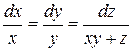 .
.
▲ Рассмотрим первую интегрируемую комбинацию
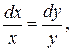
из которой можно легко найти первый интеграл исходной системы:
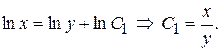
Второй интеграл исходной системы можно найти, решая уравнение
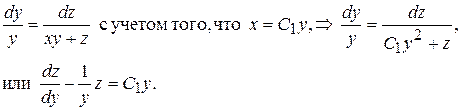
Последнее уравнение является неоднородным линейным уравнением первого порядка относительно искомой функции z, которое можно решить, используя формулу Эйлера:
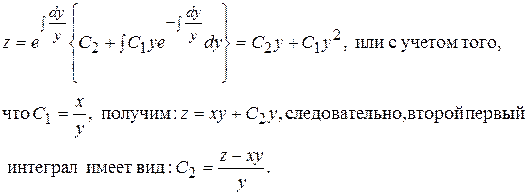
Таким образом, мы получили два первых интеграла:
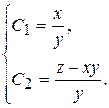 (П8.6.1)
(П8.6.1)
Третий первый интеграл можно найти из следующей комбинации
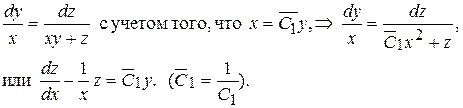
Однако, интеграл последнего уравнения линейно зависит от интеграла С 2, поэтому окончательное решение исходной системы должно быть представлено первыми двумя интегралами (П8.6.1). ▲
 2014-02-12
2014-02-12 4442
4442
