Задания для самостоятельной работы
Найти общие решения следующих однородных систем дифференциальных уравнений одним из рассмотренных методов, и произвести их проверку любым другим методом:
8.1. 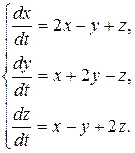 8.2.
8.2. 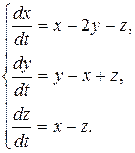
8.3. 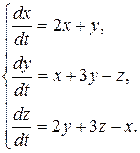 8.4.
8.4. 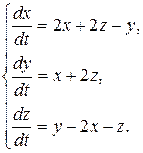
8.5. 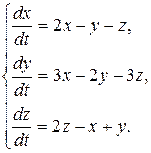 8.6.
8.6. 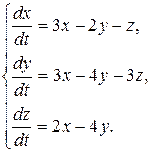
8.7. 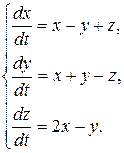 8.8.
8.8. 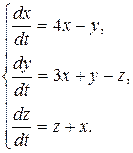
8.9. 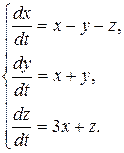 8.10.
8.10. 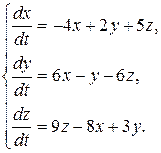
Линейная система дифференциальных уравнений имеет вид:
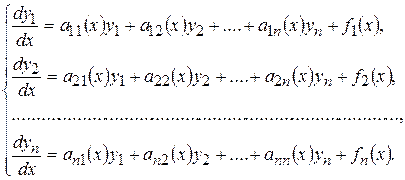 (9.1)
(9.1)
или
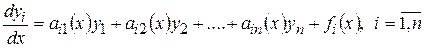 . (9.2)
. (9.2)
Системы (9.1) и (9.2) называются неоднородными, если хотя быодна из функций fi (х) не равна тождественно нулю.Если при всех значениях независимой переменной х все функции fi (х) равны нулю, то, например, система (8.14) принимает вид:
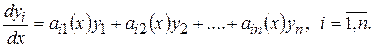 (9.3)
(9.3)
и называется однородной линейной системой.
Если все функции aij (x) и fi (х) непрерывны на отрезке a £ x £ b, то система, например, (9.2) имеет единственное решение:
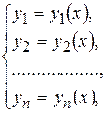 (9.4)
(9.4)
определенное во всем отрезке a £ x £ b и удовлетворяющее начальным условиям:
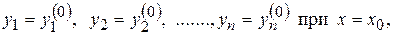 (9.5)
(9.5)
причем начальные данные 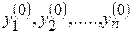 можно выбирать совершенно произвольно, а х 0 необходимо выбирать из интервала a £ x £ b.
можно выбирать совершенно произвольно, а х 0 необходимо выбирать из интервала a £ x £ b.
Неоднородная линейная система уравнений с постоянными коэффициентами имеет вид:
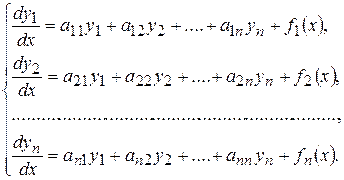 (9. 6)
(9. 6)
или
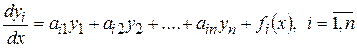 . (9.7)
. (9.7)
Если все fi (x) =0, то получим однородную систему с постоянными коэффициентами
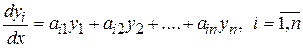 . (9.8)
. (9.8)
Если 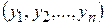 компоненты некоторого вектора
компоненты некоторого вектора 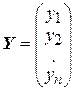 ,
,
а 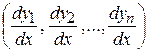 компоненты производной вектора
компоненты производной вектора 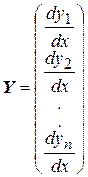 , при этом коэффициенты aij являются элементами матрицы
, при этом коэффициенты aij являются элементами матрицы 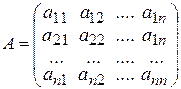 , то, например, систему уравнений (9.8) можно представить в виде:
, то, например, систему уравнений (9.8) можно представить в виде:
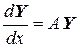 . (9.9)
. (9.9)
Рассмотрим методы интегрирования линейных систем с постоянными коэффициентами.
1. Систему дифференциальных уравнений с постоянными коэффициентами можно разрешить, например, методом Эйлера. Суть этого метода заключается в том, что решение системы (9.9) ищется в виде
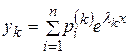 , (9.10)
, (9.10)
где λk - собственные значения матрицы коэффициентов А, которые можно найти из уравнения 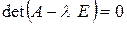 :
:
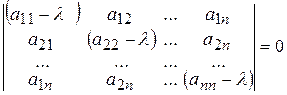 (9.11)
(9.11)
(Е – единичная матрица), которое называется характеристическим уравнением; 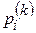 - компоненты собственного вектора P ( k )
- компоненты собственного вектора P ( k )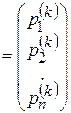 , соответствующие собственному значению λk.
, соответствующие собственному значению λk.
Если выражение (9.10) подставить в уравнение (9.9) и после сокращения на множитель 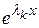 , получим однородную систему линейных алгебраических уравнений из которой можно найти вектора P ( k ):
, получим однородную систему линейных алгебраических уравнений из которой можно найти вектора P ( k ):
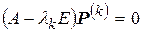 ,
,
или в развернутом виде
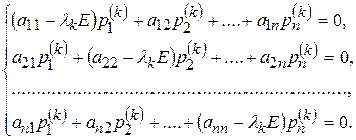 (9.12)
(9.12)
Таким образом, общее решение системы (9.9) будет выражаться формулой:
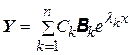 . (9.13)
. (9.13)
Из этой формулы видно, что решение исходной системы зависит от собственных значений матрицы коэффициентов λk или, что по существу то же самое от вида корней характеристического уравнения 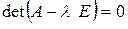 .
.
1-й случай. Все корни λk –действительные и различные, тогда общее решение системы определяется формулой (9.13). Запишем ее в развернутом виде:
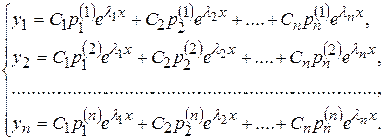 (9.14)
(9.14)
Пример 9.1.6. Найти общее решение системы
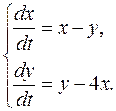
▲ Составим матрицу коэффициентов 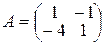 , а затем составим характеристическое уравнение (31):
, а затем составим характеристическое уравнение (31):
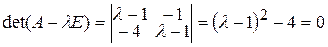 .
.
Корни этого характеристического уравнения действительные и различные: 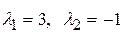 .
.
Найдем собственные вектора, соответствующие своим собственным значениям (корням характеристического уравнения).
1. 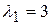 .
.
Составим систему алгебраических уравнений (9.12)
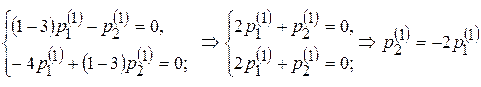 .
.
Значение 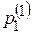 можно взять произвольно, например, пусть
можно взять произвольно, например, пусть 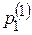 =1, тогда
=1, тогда 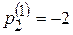 , следовательно вектор Р (1) равен: Р (1) =
, следовательно вектор Р (1) равен: Р (1) =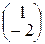 .
.
2. 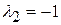 .
.
Для этого корня также составим систему (9.12)
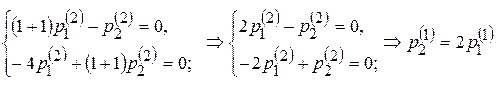 ,
,
следовательно, если 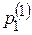 =1, тогда
=1, тогда 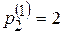 . Поэтому вектор Р (2) =
. Поэтому вектор Р (2) =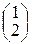 .
.
Таким образом, общее решение исходной системы можно записать в виде:
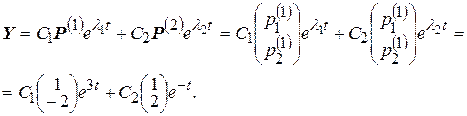
Следовательно, компоненты общего решения принимают вид:
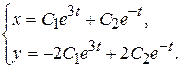 ▲
▲
2-й случай. Корни λk различные, но среди них имеются комплексные. Если 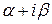 является корнем характеристического уравнения, то и
является корнем характеристического уравнения, то и 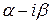 тоже будет его корнем, т.к. все коэффициенты исходной системы aij являются действительными.
тоже будет его корнем, т.к. все коэффициенты исходной системы aij являются действительными.
Компоненты общего решения системы (8.29), отвечающие корню 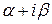 находим точно так же, как и в случае 1. Затем, отделив комплексную и действительную часть из функций yk, образующих это решение, получим два действительных решения той же системы (8.29). Сопряженный корень
находим точно так же, как и в случае 1. Затем, отделив комплексную и действительную часть из функций yk, образующих это решение, получим два действительных решения той же системы (8.29). Сопряженный корень 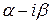 не дает новых решений (если использовать этот корень, то получим решения, линейно зависимые от уже полученных). Так поступают для каждого комплексного корня.
не дает новых решений (если использовать этот корень, то получим решения, линейно зависимые от уже полученных). Так поступают для каждого комплексного корня.
Пример 9.2. Найти общее решение системы
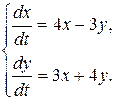
▲ Составим матрицу коэффициентов 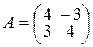 , а затем составим характеристическое уравнение (9.11):
, а затем составим характеристическое уравнение (9.11):
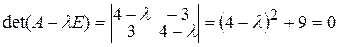 .
.
Корни этого характеристического уравнения комплексно-сопряженные: 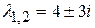 .
.
Найдем собственный вектор, соответствующий собственному значению (корню характеристического уравнения) равному: 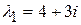 .
.
Составим систему алгебраических уравнений (9.12)
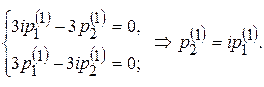
Таким образом, приняв 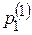 =1, находим
=1, находим 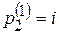 , т.е. собственный вектор Р (1) равен: Р (1) =
, т.е. собственный вектор Р (1) равен: Р (1) =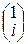 .
.
Следовательно, фундаментальная система будет иметь вид:
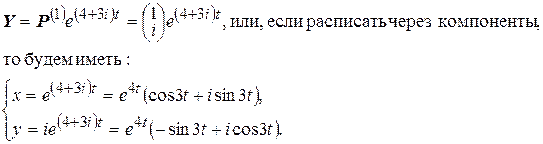
В этих решениях отделим действительную и мнимую части (корень 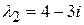 мы не рассматриваем, т.к. решения соответствующие этому корню являются линейно зависимыми корню
мы не рассматриваем, т.к. решения соответствующие этому корню являются линейно зависимыми корню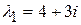 ), в результате получаем:
), в результате получаем:
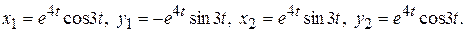
Таким образом, общее решение окончательно имеет вид:
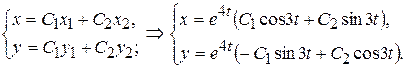
3-й случай. Среди корней характеристического уравнения имеются кратные корни.
Если корень λk, имеет кратность т, то ему соответствует п частных решений системы (9.9). Эти решения получаем в виде:
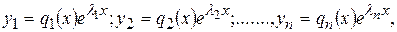
где q1 (x),…., qn (x) – многочлены от х с неопределенными коэффициентами, каждый степени не выше (т -1):
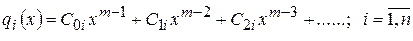 .
.
Следовательно, решения будут иметь вид:
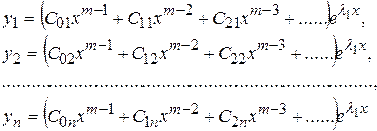 (9.15)
(9.15)
Подставляя выражения (9.15) в систему (9.9) и приравнивая коэффициенты при одинаковых степенях независимой переменной х в каждом уравнении, мы получим систему алгебраических уравнений для определения неизвестных коэффициентов многочленов q1 (x),…., qn (x). Число полученных алгебраических уравнений будет меньше числа неизвестных коэффициентов, поэтому т из этих коэффициентов остаются произвольными, а остальные выражаются через них.
Если λ 1, является комплексным числом, то полученные рассмотренным путем решения тоже будут комплексными функциями от х. Отделив в каждом из решений действительные и мнимые части, получим 2 т решений. Эти решения соответствуют паре сопряженных т – кратных комплексных корней 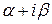 и
и 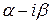 .
.
Пример 9.3. Найти общее решение системы
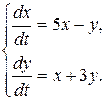
▲ Составим матрицу коэффициентов 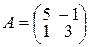 , а затем составим характеристическое уравнение (9.11):
, а затем составим характеристическое уравнение (9.11):
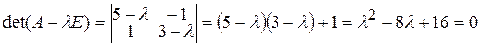 .
.
Корни этого характеристического уравнения действительные и различные: 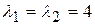 . Степень кратности т равна: т = 2. Следовательно, в этом случае многочлены p 1(t) и p 2(t) имеют вид:
. Степень кратности т равна: т = 2. Следовательно, в этом случае многочлены p 1(t) и p 2(t) имеют вид:
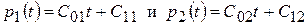 .
.
Таким образом, двукратному корню 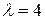 соответствует решение
соответствует решение
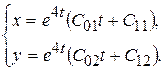
Дифференцируя х и у, получим
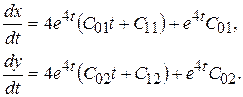
Значения х, у, 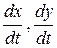 подставим в исходную систему, и после сокращения на e 4 t будем иметь
подставим в исходную систему, и после сокращения на e 4 t будем иметь
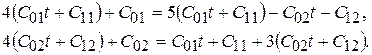
Приравнивая коэффициенты при t и свободные члены, получим следующие системы
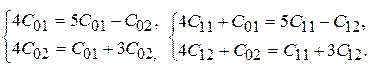
Отсюда следует, что
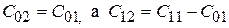 .
.
Таким образом, общее решение исходной системы будет иметь вид:
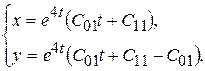 ▲
▲
2. Систему вида (9.8): 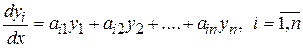 ,
,
можно разрешить методом неопределенных коэффициентов. Алгоритм этого метода следующий:
1. Составить характеристическое уравнение системы (9.8):
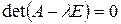 и найти его корни
и найти его корни 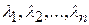 .
.
2. В зависимости от вида корней записать решение системы, причем для каждого решения yi имеет свои произвольные постоянные:
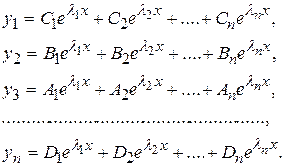
3. Вычисляются производные 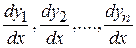 и вместе с найденными функциями
и вместе с найденными функциями 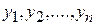 , подставляются в уравнения исходной системы.
, подставляются в уравнения исходной системы.
4. Приравниваются коэффициенты при одинаковых функциях в левых и правых частях уравнений.
5. Из полученных систем можно выразить все коэффициенты через одни, например, коэффициенты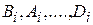 через коэффициент Ci.
через коэффициент Ci.
Пример 9.4. Найти общее решение системы
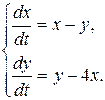
▲ 1. Составим матрицу коэффициентов 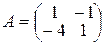 , а затем составим характеристическое уравнение (9.11):
, а затем составим характеристическое уравнение (9.11):
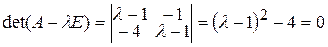 .
.
Корни этого характеристического уравнения действительные и различные 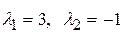 .
.
2. Исходя из этих корней общее решение исходной системы, можно записать через неопределенные коэффициенты
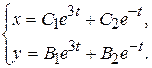
3. 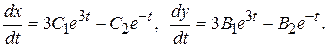
4. 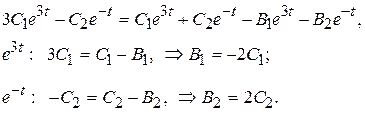
5. Таким образом, общее решение исходной системы имеет вид:
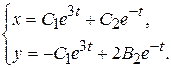
Это решение полностью совпадает с решением примера 9.1. ▲
3. Линейные системы с постоянными коэффициентами можно разрешить, также используя метод 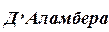 .
.
Пусть дана система
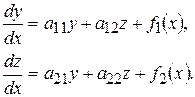 (9.16)
(9.16)
Умножим второе уравнение системы на некоторое число k и сложим почленно с первым уравнением. В результате получим
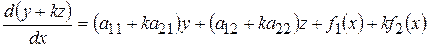 . (9.17)
. (9.17)
Необходимо преобразовать правую часть и выбрать число k так, чтобы она стала линейной функцией от y+kz. С этой цель перепишем уравнение (9.17) в виде
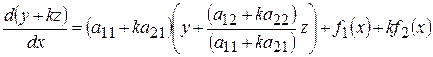 . (9.18)
. (9.18)
Далее, положив
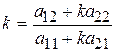 , (9.19)
, (9.19)
получим
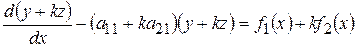 .
.
Для интегрирования этого неоднородного линейного уравнения воспользуемся формулой Эйлера [1-14]:
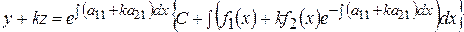 . (9.20)
. (9.20)
Если уравнение (9.19) имеет действительные и различные корни k 1 и k 2, то из формулы (9.20) получим два первых интеграла исходной системы (9.16), и на этом интегрирование исходной системы будет окончено.
Пример 9.5. Найти общее решение системы
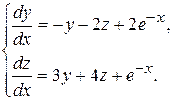
▲ Умножим второе уравнение системы на некоторое число k и сложим почленно с первым уравнением. В результате получим
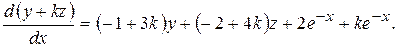
Составим уравнение (8.38)
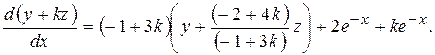
Из формулы (9.19) определим значения k
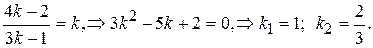
Запишем уравнение (9.18) для 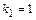
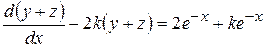
и проинтегрируем его, используя формулу (9.20)
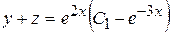 .
.
Следовательно, первый интеграл исходной системы имеет вид:
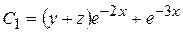 .
.
Теперь запишем уравнение (9.18) для 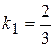
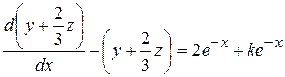
и проинтегрируем его, используя также формулу (9.20)
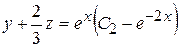 .
.
Следовательно, второй первый интеграл исходной системы равен:
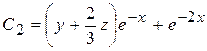 .
.
Таким образом, общий интеграл исходной системы имеет вид:
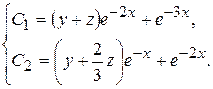 ▲
▲
Пример 9.6. Найти общее решение системы
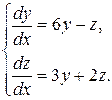
▲ Составим характеристическое уравнение системы и найдем его корни
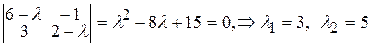 .
.
6. Запишем общее решение исходной системы:
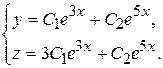 ▲
▲
 2014-02-12
2014-02-12 2894
2894
