Функциональные отношения
бинарное отношение f, действующее из X в Y называется функциональным или функцией, если для каждого элемента x из множества X существует не более одного элемента из Y, связанного этим отношением с x. Другими словами, отношение f называется функциональным, если для любого x из области определения этого отношения найдется единственный элемент y такой, что x связан с y. 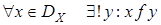 Если отношение является функциональным, то вместо Если отношение является функциональным, то вместо 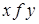 записывают, что записывают, что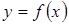 . . | 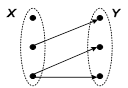 а) не функциональное отношение а) не функциональное отношение |
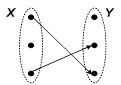 б) функциональное отношение (функция), но не отображение б) функциональное отношение (функция), но не отображение | |
В общем случае функциональное отношение действует из множества X в Y. Если функциональное отношение определено на всем множестве Х (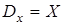 ), то оно называется отображением множества Х в множество Y. ), то оно называется отображением множества Х в множество Y. | 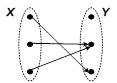 в) функциональное отображение в) функциональное отображение |
Функциональное отображение называется сюръективным или сюръекцией, если каждый элемент Y соответствует какому-то элементу X (отображение Х на Y). 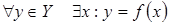 | 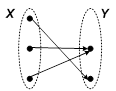 г) сюръективное отображение (сюръекция) г) сюръективное отображение (сюръекция) |
Отображение называется инъективным или инъекцией, если разным элементам x соответствуют разные элементы у. 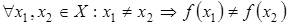 | 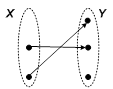 д) инъективное отображение (инъекция) д) инъективное отображение (инъекция) |
| Если отображение является одновременно сюръективным и инъективным, то оно называется биективным или биекцией (взаимно-однозначным соответствием). | 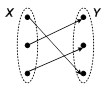 е) биективное отображение (биекция) е) биективное отображение (биекция) |
| Рис.3.1. Примеры отображений |
 2014-02-12
2014-02-12 1765
1765
