Определение 24.3. Говорят, что на множестве М точек плоскости Z задана функция
W=f(z), z=x+iy, W=u+iv, (24.3)
если указан закон, по которому каждой точке Z из М ставится в соответствие определенная точка или совокупность точек W. В первом случае функция f(z), называется однозначной, во втором – многозначной. Множество М называется множеством определения функции f(z), а совокупность N всех значений W, которые f(z), принимает на М, - множеством ее изменения. В дальнейшем наиболее важную роль будет играть тот случай, когда множества М и N являются областями.
Если положить Z=x+iy W=u+i v  , то задание функции комплексной переменной W=f(x) будет равносильным заданию двух функций двух действительных переменных:
, то задание функции комплексной переменной W=f(x) будет равносильным заданию двух функций двух действительных переменных:
U= U (x,y), V=V(x,y) (24.4)
Будем откладывать значения Z на одной комплексной плоскости, значения W-на другой. Точку функции комплексной переменной можно геометрически представлять как некоторое отображение множества M плоскости Z на множество W, и при этом двум различным точкам М всегда соответствуют различные точки N, то такое отображение называется в з а и м н о о д н о з н а ч н ы м или однолистным в М.
Пусть дана функция W=f(z), осуществляющая отображение множества M на множество N, функция Z= 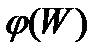 ставящая в соответствие каждой точке W из N совокупность всех тех точек Z которые функцией W=f(z) отображаются в точку W, называется обратной к функции W=f(z). Ясно, что отображение W=f(z) будет взаимно однозначным тогда и только тогда, когда обе f и
ставящая в соответствие каждой точке W из N совокупность всех тех точек Z которые функцией W=f(z) отображаются в точку W, называется обратной к функции W=f(z). Ясно, что отображение W=f(z) будет взаимно однозначным тогда и только тогда, когда обе f и  однозначны.
однозначны.
Пусть дана функция W=f(z) отображает множество М на N. Функция Z=j(W), ставящая в соответствии каждой точке W из N совокупность всех тех точек Z, которые функцией W=f(z) отображаются в точку W, называется о б р а т н о й к функции W=f(z). Ясно, что отображение W=f(z) будет взаимно однозначным тогда и только тогда, когда обе функции f и j однозначны.
Пусть функция W=f(z) отображает множество M на множество N, а 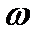 =g(w)- множество N на P. Функция
=g(w)- множество N на P. Функция
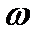 =һ(w)=g[f(z)] (24.5)
=һ(w)=g[f(z)] (24.5)
отображающая М на Р, называется сложной функцией составленной из f и g, а соответствующее отображенией h – суперпозицией отображений f и g.Если в частности отображение W=f(z), взаимно однозначно и функция Z= 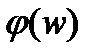 -
-
обратная к f, то
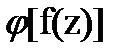 =Z (24.6)
=Z (24.6)
Пример.24.1 Линейная функция определяется во всей плоскости Z соотношением
W=az+b (24.7)
а 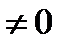 и b произвольные комплексные постоянные. Положим k =| a |
и b произвольные комплексные постоянные. Положим k =| a |  =Arg a, то есть
=Arg a, то есть
а = k(cos  +isin
+isin  ) и представим функцию (24.6) как сложную функцию, составленную из функции:
) и представим функцию (24.6) как сложную функцию, составленную из функции:
a) Z1= (cos  +isin
+isin  ) Z
) Z
б) Z2= KZ
в) W=Z2+b
 2015-03-07
2015-03-07 533
533








