Взаимная принадлежность геометрических фигур

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР

Лекция 3

Вопросы для самопроверки

1. Определителем, какого многогранника являются четыре точки, фиксированные в пространстве и не лежащие в одной плоскости?

2. Определителем, какой кривой поверхности являются четыре точки, фиксированные в пространстве и не лежащие в одной плоскости?

3. Почему проецирующую плоскость можно задать на комплексном чертеже одной ее вырожденной проекцией?

4. При каком расположении горизонталь может быть прямой профильного уровня?

В начертательной геометрии из взаимного расположения геометрических фигур наибольший интерес представляет их принадлежность друг другу и пересечение, а также частные случаи взаимного расположения, например, скрещивающиеся и параллельные прямые, эквидистантные линии и поверхности, плоскости касательные к поверхности.

Принадлежность точки и линии является одним из основных свойств параллельных проекций, которое позволяет сформулировать условие принадлежности точки и поверхности и далее линии и поверхности.

Точка принадлежит поверхности, если она принадлежит линии этой поверхности. Следовательно, для построения точки на поверхности необходимо сначала построить линию на ней, а затем точку, принадлежащую этой линии.

На рис. 18 показана точка A, принадлежащая плоской, конической и сферической поверхностям, так как она задана на линиях этих поверхностей: на плоскости Γ (p ∩ l) точка А принадлежит прямой p, на конической поверхности образующей SK, а на сферической принадлежит окружности q.

Линия принадлежит поверхности, если все ее точки принадлежат соответствующим линиям этой поверхности. На рис. 19 показана линия, расположенная на цилиндрической поверхности Σ. Она задана дискретным рядам точек (A, B, C, D, E, F), принадлежащих образующим этой поверхности.

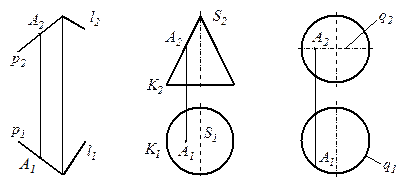
Рис. 18

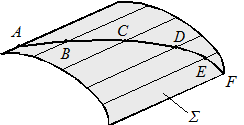
Рис. 19

Примеры принадлежности линии различным поверхностям показаны на комплексных чертежах (рис. 20):

- прямая AB принадлежит плоскости Σ (m ∩ n) (рис. 20, а);

- прямая SK - конической поверхности (рис. 20, б);

- эллипс q - цилиндрической поверхности (рис. 20, в).

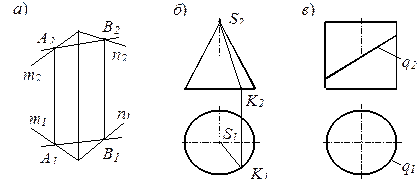
Рис. 20