Вращение вокруг прямой уровня

На рис. 33, а показана пространственная модель вращения точка А вокруг оси i, которая является прямой горизонтального уровня. В этом случае траектория вращения точки изображается на плоскость Π₁ в виде отрезка прямой А₁'А₁'', расположенного перпендикулярно горизонтальной проекции (i₁) оси и совпадающего с вырожденной проекцией (Σ₁) плоскости вращения. Положения А' и А'' точки А на траектории вращения является особыми относительно плоскости проекций Π₁, так как в этом случае точка А и ее радиус вращения АО располагаются параллельно плоскости проекция на одном и том же расстоянии от нее, что и ось вращения.

Геометрические построения на комплексном чертеже вращения точки А вокруг горизонтали i приведены на рис. 33, б. Для поворота точки А из исходного в положение, например, в положение А' необходимо определить величину радиуса вращения АО точки А.

В приведенном примере для этого выполнено построение прямоугольного треугольника (на рис. 33, б заштрихован) по двум катетам. Одним из катетов является горизонтальная проекция А₁О₁, а другим разность расстояний от точек А и О до плоскости Π_{1 .} Гипотенуза, в построенном треугольнике, равна величине радиуса вращения точки А.

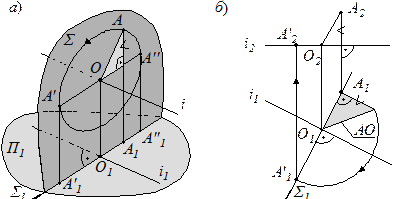
Рис. 33

Для построения горизонтальной проекции (А₁') нового положения заданной точки следует отложить полученную величину радиуса вращения от проекции О' вдоль вырожденной проекции (Σ₁) плоскости вращения. Затем строится фронтальная проекция А₂' из условия, что точка А расположена на одном уровне с осью i (см. рис. 33, б).

Следует отметить, что использование способа вращения вокруг прямой уровня при решении задач на комплексном чертеже целесообразно только в том случае, когда необходимо определить натуральную величину линейного угла или плоского многоугольника с небольшим количеством сторон. В остальных случаях рациональнее использовать другие способы преобразования проекционных чертежей.