Эйлеровы графы

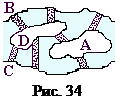
Знаменитая задача Эйлера о Кёнигсбергских мостах, сформулированная на языке графов в 1736 г., дала начало математической теории графов. Это игровая задача, суть которой заключается в следующем: в городе Кёнигсберге на реке Преголя имеется два острова, которые соединяются между собой и берегами семью мостами, как показано на рис.34. Прогуливаясь по городу и начиная движение из любой точки, требуется пройти по каждому мосту ровно по одному разу и вернуться в исходную точку.

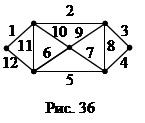
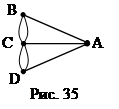Сопоставим каждому участку суши вершину графа, а каждому мосту – ребро. Тогда «план города» будет выглядеть так, как показано на рис.35. И задачу можно теперь переформулировать для графов: найти в связном графе такую замкнутую цепь, которая проходит через каждое его ребро или, как говорят, покрывает все ребра графа. Такая цепь называется эйлеровой цепью или эйлеровым циклом, а графы, в которых такая цепь существует, называются эйлеровыми графами. Очевидно, что граф, изображенный на рис.35, эйлеровым не является. Граф на рисунке 36 – эйлеров, и соответствующая эйлерова цепь – это последовательность ребер (1,2,¼,12).

Граф называется полуэйлеровым, если в нем существует открытая эйлерова цепь, т.е. цепь, покрывающая все ребра графа, у которой начальная и конечная вершины не совпадают. И, наконец, граф называется неэйлеровым, если в нем не существует ни открытой, ни замкнутой эйлеровой цепи. На рис.37 (слева) – полуэйлеров граф, на рис.37 (справа) – неэйлеров граф.

Теорема 3.13.1. Связный граф является эйлеровым тогда и только тогда, когда любая его вершина имеет четную степень.

Доказательство: (а) пусть граф является эйлеровым и С – эйлеров цикл. Тогда, проходя по ребрам С через любую вершину графа, мы увеличиваем её степень на 2, но т.к. каждое ребро графа встречается в С ровно один раз, то степень каждой вершины будет четным числом.

(б) Пусть теперь каждая вершина графа имеет четную степень, т.е. deg(v_i)³2 для любого номера вершины i. Следовательно, в графе нет висячих вершин, и он не является деревом. Поэтому в графе должен быть хотя бы один цикл, пусть это С ₁. Рассмотрим граф G ₁= G \ C ₁. Каждая вершина G ₁ должна иметь четную степень, так как все вершины C ₁ имеют степень 2. Однако, возможно, что G ₁– несвязный граф. Если G ₁ состоит только из изолированных вершин, т.е. deg(v_i)=0 для любого i, то цикл C ₁– эйлеров и теорема доказана, если же это не так, то каждая компонента G ₁– является связным графом с вершинами четной степени, и в каждой компоненте существует хотя бы один цикл. (Можно считать, что G ₁ состоит из изолированных вершин и одной связной компоненты). Пусть это циклы C ₂¹, C ₂²,¼, C ₂ ^k. Рассмотрим теперь граф G ₂= G ₁\ C ₂ , где C ₂=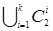. Так же, как и раньше степень каждой вершины графа G ₂– четная, либо равна нулю. Если G ₂ состоит только из изолированных вершин, то в графе имеется эйлеров цикл, который можно получить так: идем по ребрам цикла C ₁ до тех пор, пока не встретим вершину, принадлежащую какой-нибудь компоненте графа G ₁ (такие вершины обязательно есть, т.к. исходный граф связный). Далее идем по циклу этой компоненты, а затем снова продолжаем двигаться по ребрам C ₁, пока не встретим вершину следующей компоненты и переходим на ребра цикла этой компоненты, затем опять движемся по C ₁ до следующей компоненты и т.д., обойдем все ребра графа в точности по одному разу и вернемся в исходную вершину. Если G ₂ имеет неизолированные вершины, то они образуют связные компоненты, в каждой из которых есть по крайней мере один цикл C ₃¹, C ₃²,¼, C ₃ ^k. Далее рассмотрим граф G ₃= G ₂\ C ₃, где C ₃=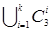. Если G ₃ состоит только из изолированных вершин, то теорема доказана, и по описанной процедуре можно указать эйлеров цикл. В противном случае удаляем из G ₃ все циклы и действуем так до тех пор, пока не будет получен граф, состоящий только из изолированных вершин.

Следствие 1: семейство ребер эйлерова графа можно разбить на непересекающиеся по ребрам циклы.

Следствие 2: каждая вершина эйлерова графа содержится хотя бы в одном цикле.

Теорема 3.13.2. В любом связном графе с 2 k нечетными вершинами имеется семейство из k цепей (не пересекающихся по ребрам), которые в совокупности покрывают все ребра графа.

Доказательство: обозначим нечетные вершины: A ₁, A ₂, ¼, A_k, B ₁, B ₂, ¼, B_k – всего 2 k вершин. Добавим к графу k ребер (A ₁, B ₁), (A ₂, B ₂),¼, (A_k, B_k). Теперь все вершины имеют четную степень, и существует эйлеров цикл. Удаляя добавленные k ребер, мы разобьем этот цикл на k цепей, содержащих все ребра исходного графа.

Следствие. Граф является полуэйлеровым тогда и только тогда, когда в нем имеется ровно две вершины нечетной степени. Очевидно, одна из этих вершин будет начальной для открытой эйлеровой цепи графа, а другая – конечной.

Рассмотрим алгоритм Флёри построения эйлеровой цепи в эйлеровом графе.

Пусть G – эйлеров граф, тогда следующая процедура всегда возможна и приводит к эйлеровой цепи графа G. Выходя из произвольной вершины, идем по ребрам графа произвольным образом, соблюдая лишь следующие правила: 1) стираем ребра по мере их прохождения и стираем также изолированные вершины, которые при этом образуются; 2) на каждом этапе идем по мосту только тогда, когда нет других возможностей.