Специальные графы

Граф называется r‑валентным или r‑однородным, если любая его вершина имеет степень, равную r.

Например, цикл является 2-валентным графом. На рисунке 32 (а) изображен 3-валентный граф Петерсона, графы Платоновых тел: (б)–куба, (в)‑тетраэдра, (г)–додекаэдра, (д)–4-валентный граф октаэдра и (е)–5-валентный граф икосаэдра.

Любой полный граф К_n, где n – число вершин, является (n‑ 1)‑ регулярным.

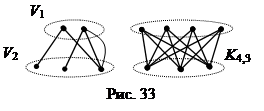Граф G= (V, E) называется двудольным, если множество его вершин V можно разбить на два непересекающихся подмножества V ₁ и V ₂, что каждое ребро графа имеет одну концевую вершину в V ₁, а вторую в V ₂. См. рис.33 слева. При этом не обязательно, чтобы каждая пара вершин из V ₁ и V ₂ была соединена ребром. Если же это так, то граф называется полным двудольным графом и обозначается обычно K_m_,_n, где m и n – число вершин в V ₁ и V ₂ соответственно. См. рис.33 справа.

В полном двудольном графе число вершин равно m + n, а число ребер m × n. Полный двудольный граф вида K _1, _n называется звездным.

Граф G= (V, E) называется k‑дольным, если множество его вершин V можно разбить на k попарно непересекающихся подмножеств V ₁, V ₂,¼, V_k, что любое ребро имеет одну концевую вершину в V_i, а вторую в V_j, где i ¹ j. Полным k ‑ дольным графом называется такой k ‑дольный граф, что любая вершина V_i смежна с любой вершиной из V_j, где i ¹ j и i, j =1,2,¼, k.