Укладкой графа на произвольной поверхности называется такое изображение его на этой поверхности, что ребра графа пересекаются только в его вершинах. Сферической укладкой называется укладка графа на сфере. Плоской укладкой называют укладку графа на плоскости.
 Граф, имеющий плоскую укладку, называется плоским. Граф, изоморфный плоскому, называется планарным. На рис.39 (а) изображен планарный граф, (б) и (в) – две его плоские укладки.
Граф, имеющий плоскую укладку, называется плоским. Граф, изоморфный плоскому, называется планарным. На рис.39 (а) изображен планарный граф, (б) и (в) – две его плоские укладки.
Теорема 3.15.1. Любой простой планарный граф можно уложить на плоскости так, чтобы его ребра были прямолинейными отрезками.
Укладка графа на плоскости равносильна его укладке на сфере, поскольку существует взаимно–однозначное соответствие точек сферы и плоскости, устанавливаемое стереографической проекцией.
Два основных непланарных графа: полный граф К 5 и полный двудольный граф К 3,3 называют графами Куратовского.
Теорема 3.15.2. Граф планарен тогда и только тогда, когда он не содержит подграфа, стягиваемого к одному из графов Куратовского.
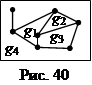 Укладка планарного графа на плоскости делит её на области, называемые гранями. Если грань имеет конечную площадь, назовем её конечной, иначе – бесконечной гранью. На рис.40 конечные грани – это g 1, g 2, g 3, а g 4 – бесконечная грань. Соотношение между числом вершин, ребер и граней в планарном графе было установлено Эйлером.
Укладка планарного графа на плоскости делит её на области, называемые гранями. Если грань имеет конечную площадь, назовем её конечной, иначе – бесконечной гранью. На рис.40 конечные грани – это g 1, g 2, g 3, а g 4 – бесконечная грань. Соотношение между числом вершин, ребер и граней в планарном графе было установлено Эйлером.
Теорема 3.15.3. (Формула Эйлера) Если связный граф планарен и имеет v вершин, r ребер и g граней, то v – r + g = 2.
Доказательство проводится индукцией по числу ребер.
Пусть r =0. Тогда в планарном связном графе имеется только одна вершина и одна бесконечная грань. И утверждение теоремы верно.
Пусть теперь теорема верна для любого связного планарного графа с (r ‑1) ребрами. Добавим к графу еще одно ребро е. При этом возможно три случая:
а) е – петля, тогда число вершин остается неизменным, число граней увеличивается на единицу, и, поскольку число ребер также увеличилось на единицу, формула остается верной;
б) е соединяет две различные вершины графа. Тогда одна из граней расщепляется на две, добавляя единицу к g. Число вершин неизменно, а число ребер увеличилось на единицу. И теорема верна.
в) е – висячее ребро. Тогда число вершин увеличивается на единицу, число граней остается прежним и, поскольку число ребер также увеличилось на единицу, формула снова верна.
Следствие 1. Пусть G – планарный граф с v вершинами, r ребрами, g гранями и k компонентами. Тогда v – r + g = k +1.
Доказательство. Применяя теорему Эйлера для каждой отдельной компоненты, получим: (*) vi – ri + gi = 2, где i =1,2,¼, k – номер компоненты. При этом 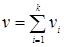 ,
, 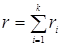 . И, поскольку для каждой компоненты учитывается бесконечная грань, то общее число граней
. И, поскольку для каждой компоненты учитывается бесконечная грань, то общее число граней 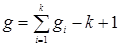 . Просуммируем (*) по числу компонент:
. Просуммируем (*) по числу компонент: 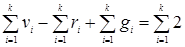 . Отсюда
. Отсюда 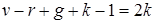 или
или 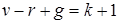 . И утверждение доказано.
. И утверждение доказано.
Следствие 2. Если G – связный простой планарный граф с r ребрами, g гранямии v вершинами, где 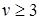 , то
, то 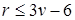 .
.
Доказательство. По теореме о степенях вершин в графе 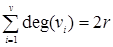 . Заметим, что каждое ребро ограничивает не более двух граней. Назовем степенью грани число ребер на её границе. Заметим, что понятие степени грани аналогично понятию степени вершины, в связи с чем можно сформулировать аналогичное утверждение о степенях граней:
. Заметим, что каждое ребро ограничивает не более двух граней. Назовем степенью грани число ребер на её границе. Заметим, что понятие степени грани аналогично понятию степени вершины, в связи с чем можно сформулировать аналогичное утверждение о степенях граней: 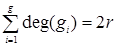 , где gi – i ‑ая грань. Поскольку граф простой, т.е. не имеет петель и параллельных ребер, и число вершин
, где gi – i ‑ая грань. Поскольку граф простой, т.е. не имеет петель и параллельных ребер, и число вершин 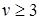 , то степень каждой грани также должна быть больше, либо равна трем. Т.е. deg(gi)³3 для любого i =1,2,¼, g. Поэтому
, то степень каждой грани также должна быть больше, либо равна трем. Т.е. deg(gi)³3 для любого i =1,2,¼, g. Поэтому 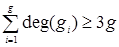 и отсюда
и отсюда 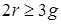 . Но из теоремы Эйлера число граней
. Но из теоремы Эйлера число граней 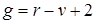 . Т.о.
. Т.о. 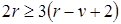 и отсюда
и отсюда 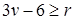 , что и требовалось доказать.
, что и требовалось доказать.
Следствие 3. Графы Куратовского K 5 и K 3,3 не являются планарными.
Доказательство. Число ребер в K 5 равно 10, число вершин – 5. И по следствию 2 получим: 9³10, что не верно. Поэтому K 5 не может быть планарным. Для графа K 3,3: r =9, v =6, а число граней по теореме Эйлера должно быть равно 9‑6+2=5. Заметим, что в графе K 3,3 нет циклов, короче 4. Поэтому степень каждой грани 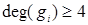 и
и 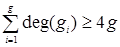 . С другой стороны
. С другой стороны 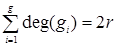 и отсюда
и отсюда 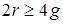 . Т.е.
. Т.е. 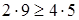 , что не верно. Поэтому K 3,3 не может быть планарным.
, что не верно. Поэтому K 3,3 не может быть планарным.
Следствие 4. В любом простом планарном графе имеется по крайней мере одна вершина степени не более 5.
Доказательство. Пусть граф имеет r ребер и v вершин. Если степень каждой вершины больше 5, то по теореме о степенях вершин 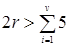 , т.е.
, т.е. 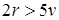 или
или 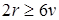 . Отсюда
. Отсюда 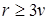 , что противоречит следствию 2, где
, что противоречит следствию 2, где 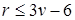 . Поэтому не все вершины графа имеют степень больше 5, и в графе имеется вершина, степень которой меньше, либо равна пяти.
. Поэтому не все вершины графа имеют степень больше 5, и в графе имеется вершина, степень которой меньше, либо равна пяти.
Свойства планарных графов используются в электротехнике. Части электрических цепей, наносимые на одну сторону непроводящей пластины, назовем «печатными схемами». Графы, соответствующие печатным схемам должны быть планарными, поскольку проводники не изолированы и не должны пересекаться. При производстве электрических схем радиоэлектронных устройств путем печатного монтажа важно знать, сколько понадобится печатных схем для комплектования всей электрической сети устройства. Наименьшее число планарных графов, объединение которых даст граф всей сети, называется толщиной графа. Толщина графа эквивалентна числу скрещиваний проводников и является мерой его непланарности. Так толщина планарного графа равна 1.
Из следствия 2 теоремы Эйлера получается оценка снизу для толщины графа, а именно: толщина простого графа 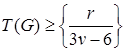 , где r и v – число ребер и вершин в графе, а фигурные скобки обозначают ближайшее справа целое число. Эта оценка довольно грубая, но, тем не менее, с помощью неё часто можно получить точные результаты. Так, например, для полного графа K 5 толщина, равная 2, полученная по этой оценке, является истинным значением.
, где r и v – число ребер и вершин в графе, а фигурные скобки обозначают ближайшее справа целое число. Эта оценка довольно грубая, но, тем не менее, с помощью неё часто можно получить точные результаты. Так, например, для полного графа K 5 толщина, равная 2, полученная по этой оценке, является истинным значением.
 2014-02-12
2014-02-12 3544
3544








