1. Даны множества: А ={ 2; 5; 8}; B ={ a; b; c }, C =(2; 5 ]. Найти: 1) A È B; 2) A È C; 3) A Ç B; 4) A Ç C; 5) A \ C; 6) C \ A; 7) A Å C; 8) A ´ B; 9) A ´ C (нарисовать); 10)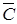 .
.
2. Найти 1)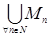 ,
, 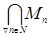 – объединение и пересечение по всем натуральным индексам n для множеств: (а) Mn ={ x Î ℝ: | x |£ n };
– объединение и пересечение по всем натуральным индексам n для множеств: (а) Mn ={ x Î ℝ: | x |£ n };
(б) Mn ={ x Î ℝ: x Î ; (в) M n = { x Î ℝ: x ¹ n }.
; (в) M n = { x Î ℝ: x ¹ n }.
3. Найти 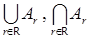 – объединение и пересечение по всем вещественным индексам r для множеств:
– объединение и пересечение по всем вещественным индексам r для множеств:
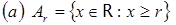 ;
; 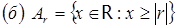 ;
;
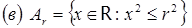 ;
; 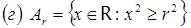 ;
;
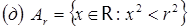 ;
; 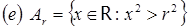 ;
;
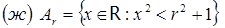 ;
; 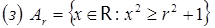 ;
;
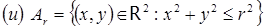 ;
; 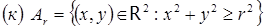 ;
;
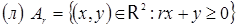 ;
; 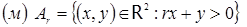 .
.
4. Докажите тождество двумя способами: а)используя диаграммы Эйлера–Венна; б) используя только определения операций над множествами. 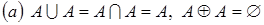 ;
;
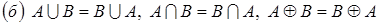 ;
;
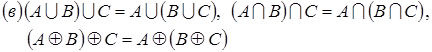
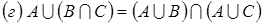 ,
,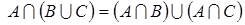 ,
,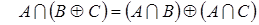 ;
;
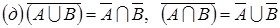 ,
,
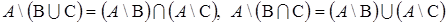 ;
;
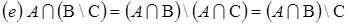 ;
;
 ;
;
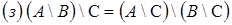 ;
;
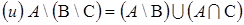 .
.
5. Доказать, что 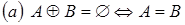 ;
; 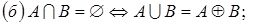
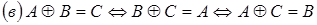 .
.
6. Определить операции 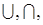 \ через: (а)Å,
\ через: (а)Å, 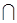 ; (б)Å,
; (б)Å, 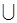 ; (в)Å, \.
; (в)Å, \.
7. Доказать, что нельзя определить: (а)\ через 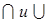 ; (б)
; (б) 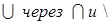 .
.
8. Найти число различных собственных разбиений множества, состоящего из четырех элементов.
Собственным разбиением множества A называется такое его разбиение на непустые и попарно непересекающиеся подмножества 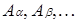 , что
, что 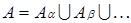 , и при этом количество этих подмножеств более одного.
, и при этом количество этих подмножеств более одного.
9. Найти число различных двухэлементных подмножеств множества, состоящего из четырех элементов. Сколько подмножеств из k элементов имеет множество, состоящее из n элементов 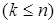 ?
?
10. Решить систему уравнений:
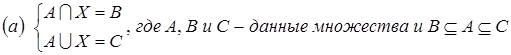 ;
;
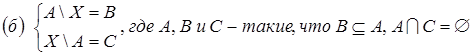 ;
;
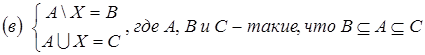 ;
;
11. Показать, чтосистема уравнений 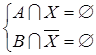 имеет решение тогда и только тогда, когда
имеет решение тогда и только тогда, когда 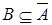 ; при этом условии решением системы является любое множество X такое, что
; при этом условии решением системы является любое множество X такое, что 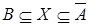 .
.
12. При каких А, В и С системы имеют решение? 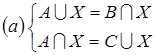

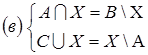
13. Выписать все элементы декартового произведения трех множеств: 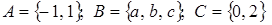 .
.
14. Найти геометрическую интерпретацию следующих множеств: (а) [ a, b ]´[ c, d ], где [ a, b ] и [ c, d ] – отрезки вещественной оси; (б) [ a, b ]2; (в) [ a, b ]3; 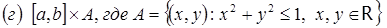 ;
; 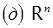 .
.
15. Сколько элементов в декартовом произведении пяти конечных множеств, состоящих из k 1, k 2, k 3, k 4 и k 5 элементов?
16. Сколько различных последовательностей длины 5 можно составить из элементов множества {‑1, 0, 1}?
17. Каково должно быть разбиение конечного множества A на два непустых и непересекающихся подмножества A 1 и A 2, чтобы декартово произведение 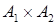 имело наибольшее число элементов?
имело наибольшее число элементов?
18. Доказать, что 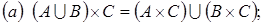
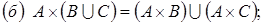
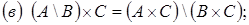
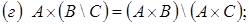
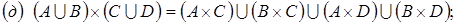
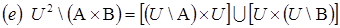
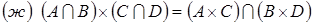
19. Доказать, что 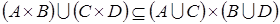 . При каких A, B, C и D получается равенство?
. При каких A, B, C и D получается равенство?
20. Даны две числовые функции: f (x)=3– x; g (x)= x 2–4. Найти: 1) ; 2)
; 2)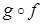 ; 3)
; 3)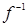 ; 4)
; 4)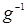 ; 5)
; 5)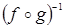 ; 6)
; 6)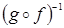 . Для множеств A =[–0.5; 2] и B =[0; 5] найти f (A), g (A), f –1(B), g -1(B). Найти также неподвижные точки отображений f и g.
. Для множеств A =[–0.5; 2] и B =[0; 5] найти f (A), g (A), f –1(B), g -1(B). Найти также неподвижные точки отображений f и g.
21. Отображение множества натуральных чисел в себя задано следующим законом: 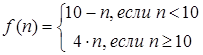 , где n – любое натуральное число. Найти образ f (ℕ) множества всех натуральных чисел.
, где n – любое натуральное число. Найти образ f (ℕ) множества всех натуральных чисел.
22. Найдите область определения, область значений бинарного отношения Р. Определите, является ли отношение Р рефлексивным, транзитивным, симметричным, антисимметричным. (а) P ={(x, y): x 2= y, где x и y – натуральные числа}; (б) P ={(x, y): x 2+ y 2=1, где x и y – целые числа }
23. Даны два множества: А ={ a, b, c } и B ={ 1,2,3,4 } и два бинарных отношения: Р 1Í А ´ В и Р2 Í В 2, где Р 1={ (a,1); (a,2); (b,3); (b,4); (c,3); (c,4) } и P 2={ (1,1); (1,4); (2,1); (2,2); (2,4); (3,3) }. Найдите: Р 1-1, Р 2-1, (Р 2° Р 1), (Р 2° Р 1)‑1, (Р 1-1° Р 2-1). Определите, является ли отношение Р 2 рефлексивным, транзитивным, симметричным, антисимметричным.
24. Выясните, какими свойствами обладает действие:
(а) умножение на множестве натуральных чисел;
(б) вычитание на множестве натуральных чисел;
(в) сложение на множестве натуральных чисел.
25. Определите, какими свойствами обладают действия обычного сложения и умножения, заданные на множестве М, образует ли множество М группу относительно какого-нибудь из этих действий, если множество М (а) { –1, 0, 1}; (б) { –1, 1}.
26. Определите, образует ли множество М ={ 0, 1 } группу относительно следующего действия: 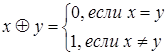 , где x и y Î M.
, где x и y Î M.
27. Составьте таблицу Кэли для сложения и умножения классов вычетов по модулю 5. Классифицируйте данную алгебраическую систему. Найдите порождающий элемент мультипликативной группы этой системы.
28. 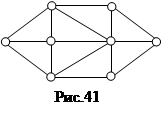 Введя необходимые обозначения, запишите матрицу смежности и матрицу инциденций для графа, изображенного на рис.41.
Введя необходимые обозначения, запишите матрицу смежности и матрицу инциденций для графа, изображенного на рис.41.
29. Найдите число ребер в абсолютном дополнении графа на рис.41. Нарисуйте это дополнение.
30. Определите степень каждой вершины в графе на рис.41 и число маршрутов длины 3 между любой парой вершин.
31. Определите циклический и коциклический ранг графа на рис.41, нарисуйте один из его остовов, изобразите соответствующее этому остову ко-дерево, а также систему фундаментальных циклов и систему фундаментальных разрезов относительно выбранного остова.
32.  Определите, является ли граф на рис.41 эйлеровым или полуэйлеровым. И, если это так, то найдите в графе эйлерову или полуэйлерову цепь соответственно. Определите также, является ли этот граф гамильтоновым, и укажите гамильтонов путь, если это так.
Определите, является ли граф на рис.41 эйлеровым или полуэйлеровым. И, если это так, то найдите в графе эйлерову или полуэйлерову цепь соответственно. Определите также, является ли этот граф гамильтоновым, и укажите гамильтонов путь, если это так.
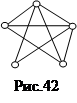
33. Определите, является ли граф на рис.42 планарным. И, если это так, то нарисуйте какую-нибудь его плоскую реализацию.
 2014-02-12
2014-02-12 1228
1228







