Методы решения линейного неоднородного д. у

Линейные дифференциальные уравнения I порядка.

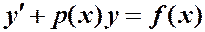
Определение. Линейное д. у. называется линейным однородным, если f (x) º 0, и линейным неоднородным, если $ x f (x) ¹ 0.

Замечание. Линейное однородное уравнение является уравнением с разделяющимися переменными (но в общем случае не является однородным д.у.):

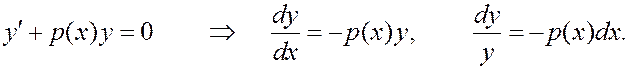
1. Метод Бернулли. Решение можно свести к решению двух уравнений с разделяющимися переменными заменой неизвестной функции на произведение двух неизвестных функций

y (x) = u (x)× v (x),

одна из которых подбирается с целью упростить уравнение.

Подставим в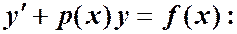

.

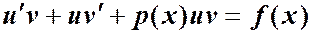Подберем функцию v (x) так, чтобы ,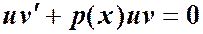

u вынесем за скобки. Учитывая, что u (x) не может тождественно равняться нулю (иначе y (x) º 0, а такого решения нет), получим

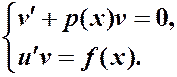
Для первого достаточно одного решения v (x), так как цель – упростить; для второго нужны все решения:

u (x, С).

y = u (x, С)× v (x).

Пример. 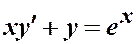, y (1) = 1.

Решение. y (x) = u (x)× v (x).

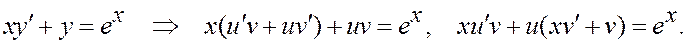
Запишем систему: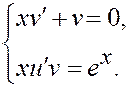

Первое уравнение:

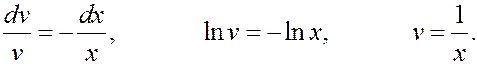
Второе уравнение:

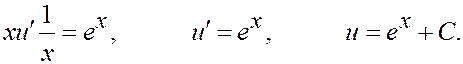
Общее решение исходного д.у.:

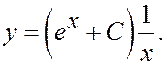
Решение задачиКоши:

Замечание. Переписав уравнение 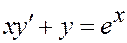в виде

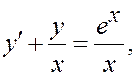
заметим, что задачу Коши y (x ₀) = y ₀ можно ставить в любой точке x ₀¹0 с любым значением y ₀.

2. Методвариации произвольной постоянной (метод Лагранжа).