Общее и частное решения, общий и частный интегралы уравнения. Особые решения

Замечание 1. Решение y (x) может оказаться найденным неявно: 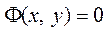или x = x (y)

(недифференциальное уравнение с теми же решениями).

Во всех этих случаях будем считать задачу решенной.

Если решение содержит «невзятые» интегралы, будем говорить, что уравнение «решено в квадратурах».

Замечание 2. Далеко не все д. у. 1-го порядка решаются, даже в квадратурах.

Определение. 1. Если в области D пл. (x, y) через каждую ее точку проходит единственная интегральная кривая y = y (x), то каждое из таких решений y (x) называется частным решением уравнения в области D. Графики частных решений не пересекаются.

2. Если получена формула

y = φ(x, C) (*)

такая, что

а) " С из некоторого E Í R функция y = φ(x, C) есть частное решение в D,

б) наоборот, каждое частное решение в D может быть получено по этой формуле выбором единственного надлежащего С, то формула (*) называется общим решением д. у. в D.

Определение. Частные решения называют также частными интегралами, а общее решение – общим интегралом д. у. Но чаще термины частный интеграл и общий интеграл применяются в случаях, когда частное и общее решения определяются неявно:

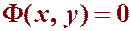и ,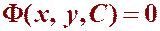

с теми же решениями, что и исходное д. у.

Замечание 3. По границе области D, для которой получено общее решение, также может проходить интегральная кривая, причем как со свойством единственности в каждой точке (такое решение будем также называть частным), так и с нарушением единственности в каждой точке (такое решение будем называть особым).

Примеры. 1. 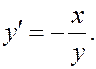y ¹ 0.

Д. у. задает поля направлений в двух полуплоскостях:

y > 0 и y < 0.

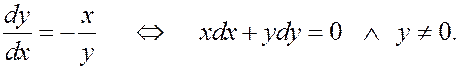
В левой части – полный дифференциал функции

Þ

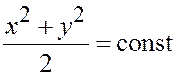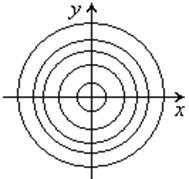Интегральные кривые д. у. в верхней полуплоскости: верхние полуокружности, в нижней: нижние полуокружности.

– общий интеграл уравнения в каждой полуплоскост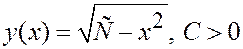и,

и 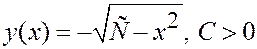– общие решения.

2. 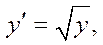y ³ 0.

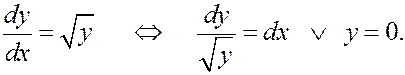
y = 0 – решение, его график проходит по границе области. Найдем другие решения.

y (x) Þ

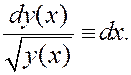
Интегрируя обе части уравнения: правую часть по x, а левую по y (в силу инвариантности интегральных формул), получим две первообразные функции, отличающиеся на константу: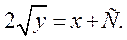

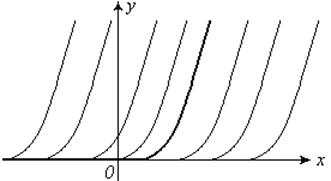
Это общее решение в полуплоскости y > 0.

Решение y = 0 – особое. В полуплоскости y ³ 0 есть решения, не являющиеся ни частными, ни особыми.

18.1.5. Теорема о существовании и единственности решения д. у. .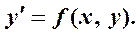

Теорема. Если в области D плоскости (x, y) функции

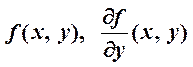
непрерывны, то через каждую точку области D проходит единственная интегральная кривая уравнения

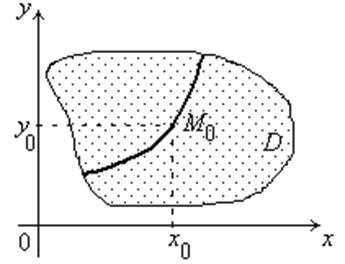
Другими словами, при выполнении условий теоремы для любой точки (x ₀, y ₀)Î D существует единственное решение y (x) на некотором интервале оси Ox, содержащем точку x ₀, такое, что y (x ₀) = y ₀.