Д. у. с разделяющимися переменными.
Некоторые типы д. у. I порядка и методы их решения.
Задача Коши для д. у. I порядка.
Определение. Задачей Коши для д. у. I порядка в области D называют задачу нахождения решения y (x), удовлетворяющего начальному условию y (x 0) = y 0.
Геометрически это означает, что ищется интегральная кривая, проходящая через т. M 0(x 0, y 0)Î D.
Теорема дает условия $-я и единственности решения задачи Коши 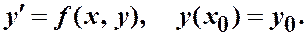
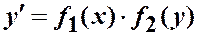
или
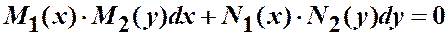
Метод решения. Разделение переменных:
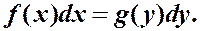
При непрерывных функциях f (x) и g (y) это равенство дифференциалов (тождественное равенство при подстановке решения y = y (x)).
Þ находим первообразные, интегрируя левую часть по x, а правую – по y (инвариантность интегральных формул):
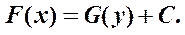
Это общий интеграл д. у., так как это уравнение имеет то же множество решений, что и исходное д.у.
Если решается задачи Коши:
подставить в общий интеграл x 0, y 0, найти С 0 и
записать частный интеграл
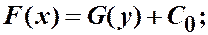
Пример. 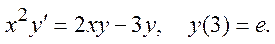
Преобразуем:
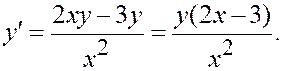
Д. у. можно решать в полуплоскостях x > 0 и x < 0.
Задача Коши поставлена в полуплоскости x > 0.
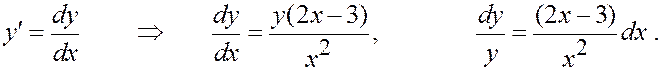
Могли потерять решение y = 0 (делили).
Подставим это выражение в уравнение: убеждаемся, что оно удовлетворяет уравнению, откуда следует, что оно– решение.
Þ Искомое решение y (x) > 0 (в силу единственности интегральные кривые не пересекаются).
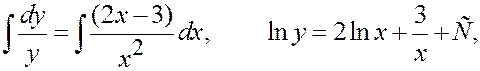
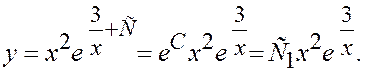
x = 3, y = e Þ 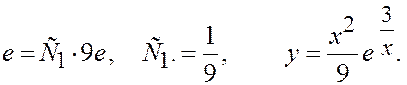
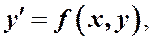 если f (l x, l y)= f (x, y) (1)
если f (l x, l y)= f (x, y) (1)
или
если $ m Î R:
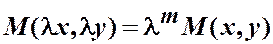 ,
, 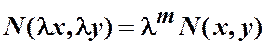 .
.
Уравнение однородное, если оно не меняется при подстановке l x вместо x и l y вместо y (в производные и дифференциалы не подставляем!)
Пример. 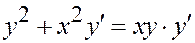
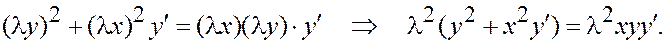 Сокращая на l2, получим исходное уравнение.
Сокращая на l2, получим исходное уравнение.
Метод решения. Однородное уравнение сводится к уравнению с разделяющимися переменными заменой неизвестной функции
y (x) = x × u (x). (*)
Покажем это.
1) 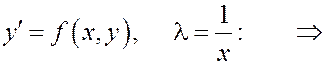
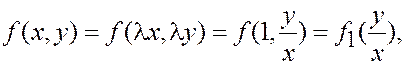
Þ
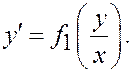
2) 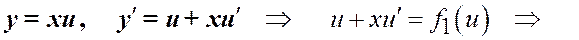
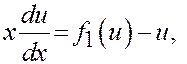
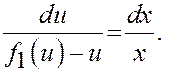
Переменные разделены.
Замечание. В процессе преобразования уравнений нужно следить, не потерялись ли решения и не появились ли лишние.
Пример. 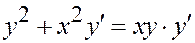 .
.
Решение. 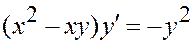 .
.
Можно выразить y ¢, но можно и сразу сделать замену неизвестной функции:

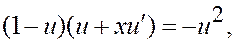

(уравнение с разделяющимися переменными).
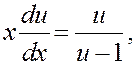
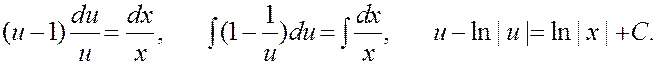
Вернемся к первоначальным переменным:
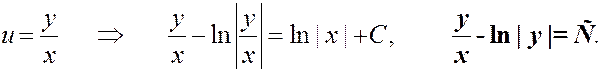
Получен общий интеграл д. у.
Мы делили на u. Проверим, не потеряно ли решение
y = 0, соответствующее значению: u = 0. Подстановка константы y = 0 превращает исходное уравнение
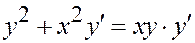
в тождество: 0+0=0. Это решение, которое нельзя получить из общего решения.
 2014-02-12
2014-02-12 471
471








