Примеры точечных групп симметрии

Примитивные ячейки. Примитивная ячейка – элементарная ячейка минимального объема. На примитивную ячейку приходится только один узел решетки Браве. Существует много способов выбора примитивной ячейки и примитивных трансляций. Объем всех примитивных ячеек одинаков. Число атомов в примитивной ячейке равно числу атомов базиса.

К каждой частице, находящейся в кристалле, примыкает вплотную только определенное число соседних частиц. Это число ближайших соседних частиц называется координационным числом. Основными параметрами, характеризующими кристаллическую структуру, некоторые из которых взаимосвязаны, являются следующие:

• тип кристаллической ячейки (сингония);
• число формульных единиц, приходящихся на элементарную ячейку;
• параметры элементарной ячейки (линейные размеры и углы);
• координаты атомов в ячейке;
• пространственная группа;
• координационные числа всех атомов.

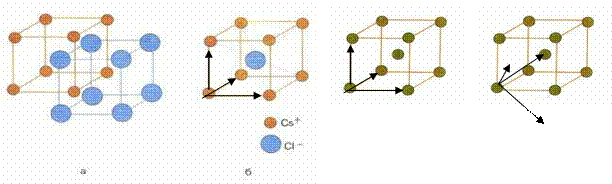Ниже показаны примеры элементарной и примитивной ячеек кубической решетки CsCl (простая кубическая решетка Браве с базисом из 2 атомов) и Na (элементарная ячейка объемноцентрированной кубической решетки Браве с базисом из 2 атомов Na и примитивная ячейка с базисом из 1 атома Na).

Рис.2. CsCl (корд. число 8 по цезию и по хлору, 1 формульная единица на элементарную ячейку). Ячейка Na (коорд. число 8, 2е формульные единицы на элементарную ячейку, 1 форм. Ед. на примитивную ячейку)

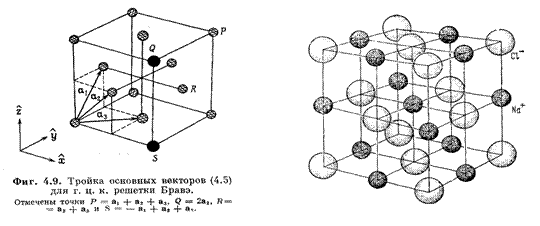
Разнообразие кристаллических структур связано с наличием в базисе атомов различной конфигурации. Например, о.ц.к. решетка Браве с базисом из двух одинаковых атомов в элементарной ячейке переходит в простую кубическую решетку Браве, если имеет в базисе два различающихся атома как в случае CsCl. Наоборот NaCl – содержит две вложенные г.ц.к. решетки, но при одинаковых атомах – структура образует простую кубическую решетку. Алмаз Fd3m с 8 атомами в ячейке (базис)и Сфалерит Fm (ZnS) – г.ц.к. с 8 атомами в ячейке (В примитивной ячейке – 2 атома).

Тип базиса Группа симметрии	Решетка Браве (базис из 1 атома-сферическая симметрия)	Кристаллическая структура Произвольный базис
Число точечных групп (повороты, отражения, инверсия)	7 сингоний (7 голоэдрических точечных групп)	32 точечные группы
Число пространственных = точечная +трансляционная	14 решеток Браве	230 групп Федорова

Рис. 3. Элементарная ячейка и векторы трансляций примитивной ячейки кристаллической решетки Браве (слева) для плотной гранецентрированной кубической упаковки NaCl (справа). Кристаллическая структура NaCl состоит из двух вложенных г.ц.к. решеток Браве, так как базис решетки Браве состоит из двух атомов Na и Cl. Выбранная элементарная ячейка структуры (справа) содержит четыре формульные единицы NaCl. Координационные числа для Na – 6 и Сl - 6. Координаты атомов базиса: Na (000), (1/2,1/2,0), (1/2,0,1/2), (0,1/2,1/2) Cl (1/2,1/2,1/2), (0,0,1/2), (0,1/2,0), (0,0,1/2).

Возможные типы решеток Браве.

Кристаллы характеризуются симметричным расположением атомов, которое инвариантно не только относительно трансляций, но и относительно других операций симметрии – вращений, отражений, инверсии. Совокупность таких операций может обладать групповыми свойствами, которые описываются в теории групп.

Пространственная группа симметрии, федоровская группа, совокупность преобразований симметрии, присущих атомной структуре кристаллов (кристаллической решётке). Вывод всех 230 пространственных групп был осуществлен в 1890—91 русским кристаллографом Е. С. Федоровым и независимо от него немецким математиком А. Шёнфлисом. Преобразованиями (операциями) симметрии называются геометрические преобразования различных объектов (фигур, тел, функций), после которых объект совмещается сам с собою. Поскольку кристаллическая решётка обладает трёхмерной периодичностью, то для пространственной симметрии кристаллов характерной является операция совмещения решётки с собой путём параллельных переносов в 3 направлениях (трансляций) на периоды (векторы) а, b, с, определяющие размеры элементарной ячейки. Другими возможными преобразованиями симметрии кристаллической структуры являются повороты вокруг осей симметрии на 180°, 120°, 90° и 60°; отражения в плоскостях симметрии; операция инверсии в центре симметрии, а также операции симметрии с переносами (винтовые повороты, скользящие отражения и некоторые др.). Операции пространственной симметрии могут комбинироваться по определённым правилам, устанавливаемым математической теорией групп, и сами составляют группу.

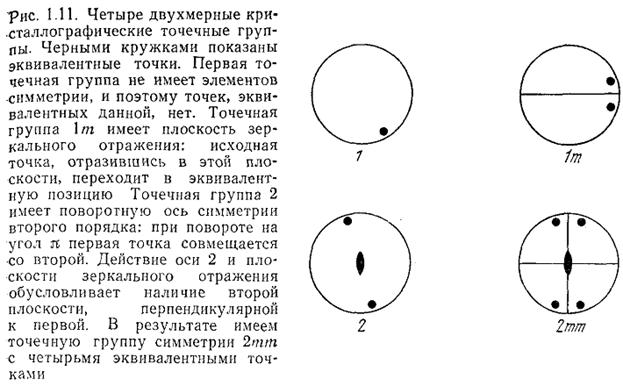
Группы симметрии, oперации которых оставляют хотя бы одну точку пространства на месте, называются точечными группами симметрии. Типичные примеры точечных групп — группа вращений, группа линейных преобразований, зеркальная симметрия.

Точечная группа определяет симметрию тензоров используемых для описания электрических, оптических, магнитных и др. свойств кристалла