2014-02-12
517
Для двумерной случайной величины (Х, Y) можно ввести так называемое условное математи-ческое ожидание Y при Х = х. Для дискретной случайной величины оно определяется как
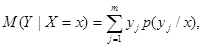(11.7)
для непрерывной случайной величины –
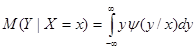. (11.8)
Определение 11.4. Функцией регрессии Y на Х называется условное математическое ожидание
M (Y / x) = f (x).
Аналогично определяется условное математическое ожидание Х и функция регрессии Х на Y.
Определение 11.5. Если обе функции регрессии Х на Y и Y на Х линейны, то говорят, что Х и Y связаны линейной корреляционной зависимостью.
При этом графики линейных функций регрессии являются прямыми линиями, причем можно доказать, что эти линии совпадают с прямыми среднеквадратической регрессии.
Теорема 11.2. Если двумерная случайная величина (Х, Y) распределена нормально, то Х и Y связаны линейной корреляционной зависимостью.
Доказательство. Найдем условный закон распределения Y при Х = х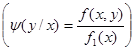 
, используя формулу двумерной плотности вероятности нормального распределения (11.1) и формулу плотности вероятности Х:
|
|
|
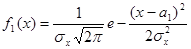. (11.9)
Сделаем замену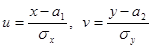 
. Тогда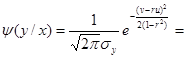 
=
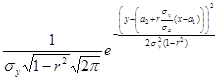. Полученное распределение является нормальным, а его мате-матическое ожидание 
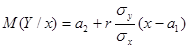есть функция регрессии Y на Х (см. опреде-ление 11.4)). Аналогично можно получить функцию регрессии Х на Y:
.
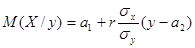Обе функции регрессии линейны, поэтому корреляция между Х и Y линейна, что и требовалось доказать. При этом уравнения прямых регрессии имеют вид
, 
,
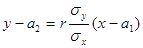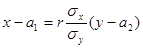то есть совпадают с уравнениями прямых среднеквадратической регрессии (см. формулы (11.5), (11.6)).
