Транспортная модель при различных условиях погашения задолженности

Пусть срок кредита равен k_ij (платежных периодов). В дальнейшем при записи формул будем полагать ставку процентов годовых Е_ij, переведенной в доли единицы. В случае погашения долга равными срочными уплатами в конце расчетного периода остаток основного долга и суммы процентных платежей уменьшаются от периода к периоду, годовой расход погашенного основного долга растет, а срочные уплаты являются аннуитетами ренты постнумерандо.

Воспользуемся формулой определения срочной уплаты П_ij в счет погашения задолженности за финансовые ресурсы, предоставленные i -м банком на приобретение материалов j -го наименования:

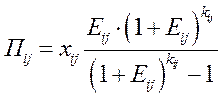, (3.6)

где величина:

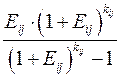(3.7)

является коэффициентом погашения задолженности перед i -м банком.

Тогда, если все П_ij равны между собой, наращенная сумма по кредиту, предоставленному i -м банком на приобретение материалов j -го наименования, равна:

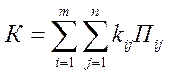, (3.8)

Следовательно, целевая функция может быть записана так:

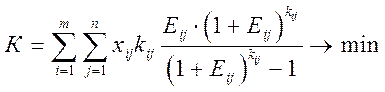. (3.9)

Коэффициенты при неизвестных в целевой функции можно записать в матрицу (табл. 3.4).

Таблица 3.4

Матрица коэффициентов при неизвестных в целевой функции при погашении долга равными срочными уплатами

Банки	Коэффициенты при неизвестных в целевой функции при погашении долга аннуитетами	Предло-жение капитала
		…	j	…	n
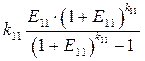
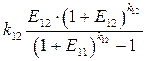
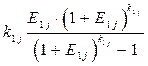
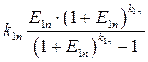
			…		…		d 1
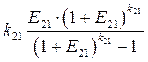
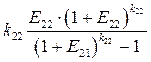
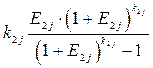
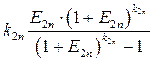
			…		…		d 2
…	…	…	…	…	…	…	…
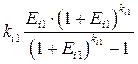
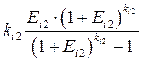
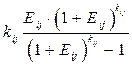
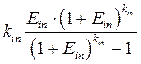
i			…		…		di
…	…	…	…		…	…	…
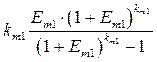
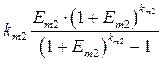
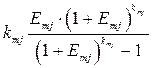
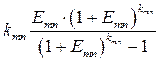
m			…		…		dm
Спрос на капитал	b 1	b 2	…	bj	…	bn

Если в кредитном договоре оговорено погашение основного долга равными ежегодными платежами, то наращенная сумма долга К_ij i -му банку за предоставленные заемные средства на приобретение материалов j -го наименования вычисляется так:

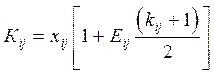. (3.10)

Полученная матрица коэффициентов при неизвестных в целевой функции представлена в табл. 3.5. Тогда, целевую функцию можно сформулировать так:

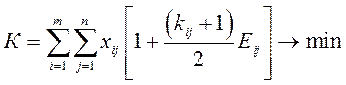. (3.11)

Если банки используют различные схемы погашения задолженности, то при записи целевой функции целесообразно обозначить коэффициент при неизвестных l_ij. Это позволяет записывать целевую функцию в более удобной форме:

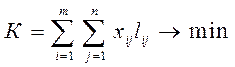, (3.12)

где l_ij принимает любые значения в зависимости от применяемой схемы погашения задолженности.

Предположим, что банк 1 использует обычную схему погашения задолженности для финансирования приобретения материалов j -го наименования, банк 2 применяет погашение займа равными выплатами основного долга, а остальные банки − аннуитет. Запишем коэффициенты при неизвестных.

Для банка 1:

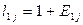. (3.13)

Для банка 2:

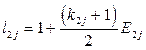. (3.14)

Для остальных банков:

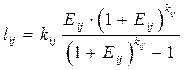. (3.15)

где i ≠ 1,2.

Таблица 3.5

Матрица коэффициентов при неизвестных в целевой функции при условии погашения займа

равными выплатами основного долга

Банки	Коэффициенты при неизвестных в целевой функции при условии погашения займа равными выплатами основного долга	Предло-жение капитала
		…	j	…	n
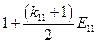
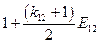
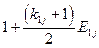
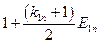
			…		…		d 1
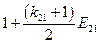
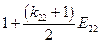
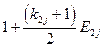
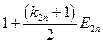
			…		…		d 2
…	…	…	…	…	…	…	…
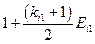
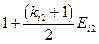
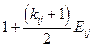
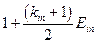
i			…		…		di
…	…	…	…		…	…	…
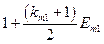
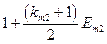
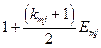
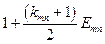
m			…		…		dm
Спрос на капитал	b 1	b 2	…	bj	…	bn