С учетом соответствующего числа степеней свободы могут быть получены оценки соответствующих дисперсий.
Для общей дисперсии:
rобщ = N–1 = m1×m2×n–1
Для факторной дисперсии (фактор х1):
r1 = m1–1
Для факторной дисперсии (фактор х 2):
r2 = m2–1
Для дисперсии взаимодействия:
r12 = m1×m2–(m1+m2–1) = < проще как, произведение числа независимых слагаемых каждой å > = (m1–1)×(m2–1) =m1×m2–(m1–1)–(m2–1)–1= m1×m2–(m1+m2)+1 (+1 – т.к. все 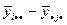 связаны через
связаны через 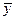 )
)
Для остаточной дисперсии:
rост = N–m1×m2
Выполняется:
rост = r1+r2+r12+rобщ
Оценки дисперсий будут равны:
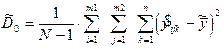 – общая;
– общая;
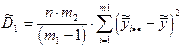 – факторная (фактора х 1);
– факторная (фактора х 1);
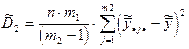 – факторная (фактор х 2);
– факторная (фактор х 2);
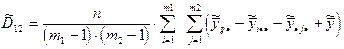 – взаимодействия;
– взаимодействия;
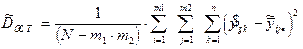 – остаточная.
– остаточная.
Т.к. ошибка наблюдения e подчинена нормальному закону распределения с me = 0; De = s2, кроме того выполняется равенство: rост = r1+r2+r12+rобщ, то можно показать, что вариации S21, S22, S212, S2ост, S2общ подчинены s2c2 распределению с соответствующими числами степеней свободы.
 2014-02-13
2014-02-13 501
501








