Основы регрессионного анализа

Лекция 5

Задачей регрессионного анализа является выявление зависимости (вида стохастической взаимосвязи) результатов наблюдений от случайных или неслучайных входных воздействий. Так как планирование эксперимента предполагает активный эксперимент с возможностью управления значениями входных факторов, ограничимся случаем, когда значения входных переменных x₁,...,x_k неслучайны и точно известны, а результат наблюдения случайная величина, т.е. .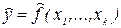

Сущность регрессионного анализа состоит в замене стохастичес­кой зависимости 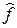между результатами наблюдений и переменными x_i некоторой детерминированной зависимостью 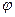, достаточно хорошо апп­роксимирующей основные свойства исходной стохастической зависимос­ти. В качестве характеристики случайной величины 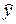, для которой в регрессионном анализе устанавливается такая зависимость, исполь­зуется ее условное математическое ожидание: 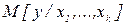, а в качестве зависимости 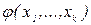- уравнение регрессии или по­верхность отклика, т.е. 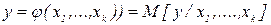(отсюда и название - регрессионный анализ).

Как известно, основным свойством уравнения регрессии является то, что средний квадрат отклонения случайной величины у от линии регрессии всегда меньше, чем от любой другой кривой, т.е. 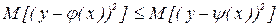для любого 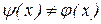, где 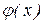- уравне­ние регрессии, x=(x₁,…,x_k).

Отсюда следует, что если вид функции 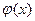известен, но неизвестны ее параметры, то их можно находить используя метод наименьших квадратов. т.е. минимизируя 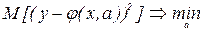где - параметры кривой .

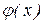Поскольку на практике в общем случае вид зависимости 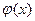априорно неизвестен, то первоначально производится ее выбор среди заданных классов функций (линейные, полином r-го порядка и т.д.) исходя из физической природы самой задачи. Методы регрессионного анализа позволяют лишь найти ее параметры и оценить, насколько удачен выбор.

Оценка функции 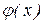в заданном классе функций 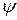, минимизирующая квадрат отклонений, называется среднеквадратической регрессией в классе 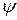Для определения ее параметров используется МНК.

По числу независимых переменных x_i регрессионный анализ подразделяется на однофакторный (одна входная переменная) и многофакторный - несколько входных переменных (факторов).

В регрессионном анализе рассматриваются только количествен­ные управляемые переменные x_i.

По виду функции, описывающей связь между входными переменными х и результатам наблюдений у, различают линейный и нелинейный рег­рессионный анализ Если вид функции априорно неизвестен, то перво­начально стараются применять линейные модели. Если же их использо­вание не позволяет получить приемлемых результатов, то переходят к нелинейным моделям.

В общем случае часто используется модель (линейная относи­тельно неизвестных коэффициентов) вида

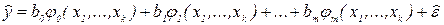
где b₀,..., b_m - неопределенные параметры модели; x₁,..., x_k -независимые переменные; 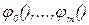- некоторые известные функции; 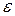- ошибка результатов наблюдений, появляющаяся за счет действия неучтенных факторов (ошибка измерений).

Линейная форма связи переменных х и у на практике весьма распространена и к ней можно свести и нелинейные по сути модели, используя линеаризирующие их преобразования. Например:

1. Мультипликативная модель: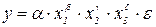
Прологарифмировав, получим

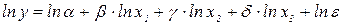
2. Экспоненциальная модель: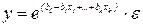

Отсюда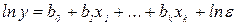

3. "Обратная" модель: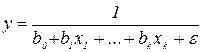

или иначе 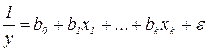и т.п.